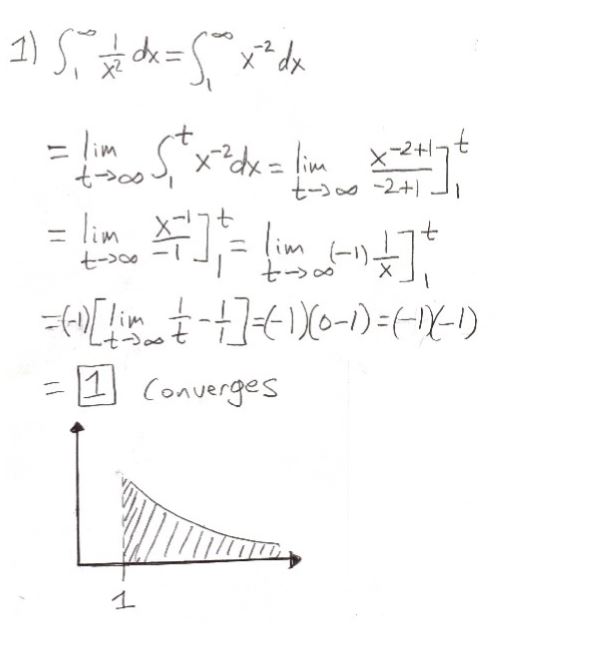
1. Identify the Improper Integral:

\(\int_{1}^{\infty} \frac{1}{x^2} \,dx\)

This integral is improper because the upper limit of integration is infinity. We want to find the area under the curve of \(\frac{1}{x^2}\) from 1 to infinity.

2. Rewrite Using a Limit:

\(\lim_{b \to \infty} \int_{1}^{b} \frac{1}{x^2} \,dx\)

We introduce a variable upper bound \(b\) to replace infinity and express the integral as a limit. This allows us to work with a finite upper bound and then take the limit as it approaches infinity.

3. Find the Antiderivative:

The antiderivative of \(\frac{1}{x^2}\) is \(-\frac{1}{x}\).

We find the antiderivative by recognizing that \(\frac{1}{x^2}\) is the derivative of \(-\frac{1}{x}\), so we can use this expression to evaluate the integral.

4. Evaluate the Integral with Variable Bound:

\(\lim_{b \to \infty} \left[ -\frac{1}{x} \right]_{1}^{b}\)

We apply the Fundamental Theorem of Calculus by evaluating the antiderivative at the bounds 1 and \(b\), then taking the difference.

5. Substitute the Bounds:

\(\lim_{b \to \infty} \left( -\frac{1}{b} + \frac{1}{1} \right)\)

We substitute the bounds into the antiderivative, replacing \(x\) with \(b\) and 1, and then simplify the expression.

6. Evaluate the Limit:

\(\lim_{b \to \infty} \left( -\frac{1}{b} \right) + 1 = 0 + 1 = 1\)

As \(b\) approaches infinity, the term \(-\frac{1}{b}\) approaches 0, so the entire limit evaluates to 1.

Conclusion: The improper integral of \(\frac{1}{x^2}\) from 1 to infinity is 1.

This result tells us that the area under the curve of \(\frac{1}{x^2}\) from 1 to infinity is finite and equal to 1.