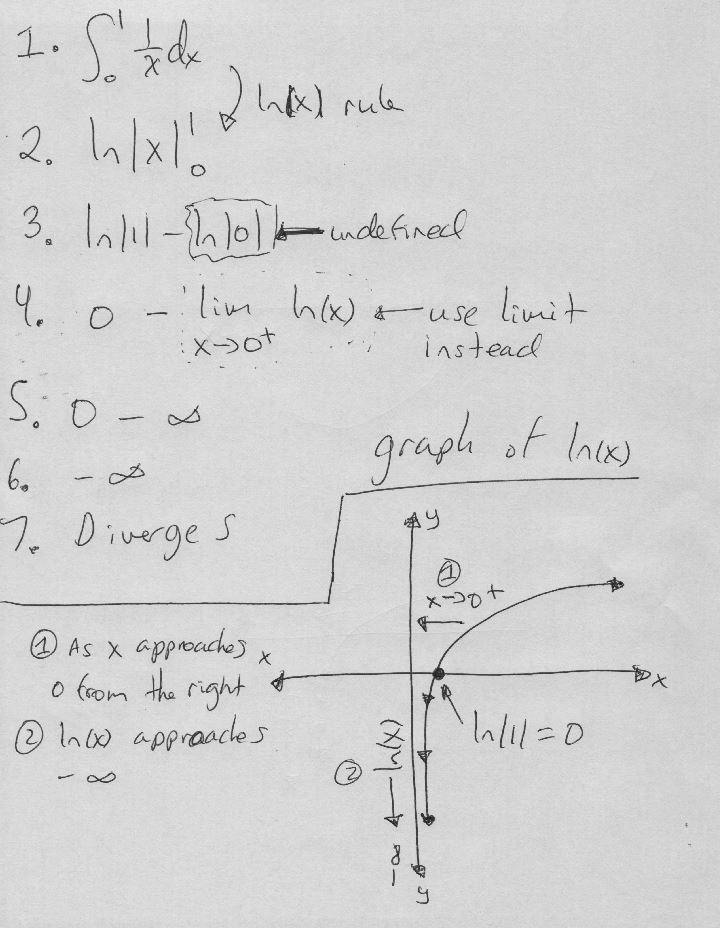
Finding the Integral of 1/x from 0 to 1

Step 1: Identify the Function and Limits

We are dealing with the function \( \frac{1}{x} \) and we want to find its integral from 0 to 1. The integral is represented as ∫₀¹ \( \frac{1}{x} \) dx.

Step 2: Recognize the Improper Integral

This is an improper integral because the function \( \frac{1}{x} \) is undefined at \( x = 0 \). We’ll need to approach this limit carefully.

Step 3: Set Up the Limit

To handle the undefined point at \( x = 0 \), we’ll use a limit. We’ll integrate from \( \epsilon \) to 1, and then take the limit as \( \epsilon \) approaches 0.

Step 4: Integrate \( \frac{1}{x} \)

The integral of \( \frac{1}{x} \) with respect to \( x \) is \( \ln |x| \).

Step 5: Apply the Limits

We need to evaluate \( \ln |x| \) at the upper and lower limits, which are 1 and \( \epsilon \). This is represented as \( \ln |x| \) |ₑ¹.

\( \ln(1) = 0 \)

\( \ln(\epsilon) = \ln(\epsilon) \)

Step 6: Subtract the Lower Limit from the Upper Limit

0 – \( \ln(\epsilon) = -\ln(\epsilon) \)

Step 7: Take the Limit

As \( \epsilon \) approaches 0, \( -\ln(\epsilon) \) approaches \( -\infty \).

Final Result

The integral of \( \frac{1}{x} \) from 0 to 1 is divergent and approaches \( -\infty \).