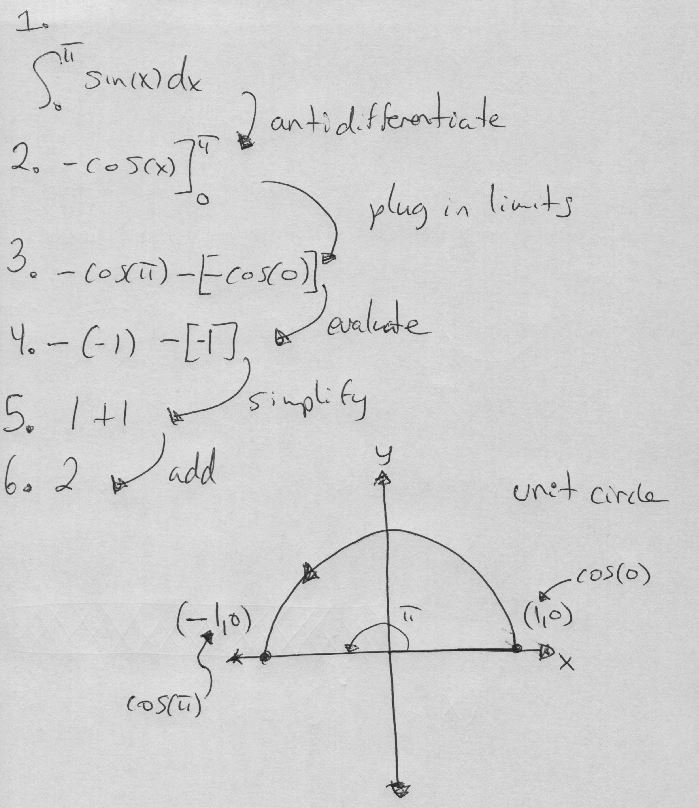
Finding the Integral of sin(x) from 0 to π

Step 1: Identify the Function

We are dealing with the function sin(x) and we want to find its integral from 0 to π. The integral is represented as ∫₀ᴨ sin(x) dx.

Step 2: Integrate sin(x)

The integral of sin(x) with respect to x is -cos(x).

Step 3: Apply the Limits

We need to evaluate -cos(x) at the upper and lower limits, which are π and 0. This is represented as -cos(x) |₀ᴨ.

-cos(π) = 1

-cos(0) = -1

Step 4: Subtract the Lower Limit from the Upper Limit

1 – (-1) = 2

Final Result

The integral of ∫₀ᴨ sin(x) dx is 2.