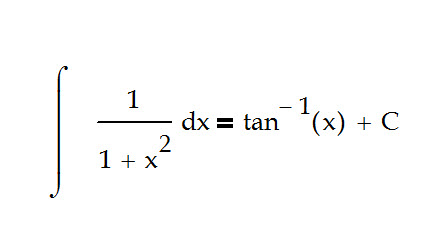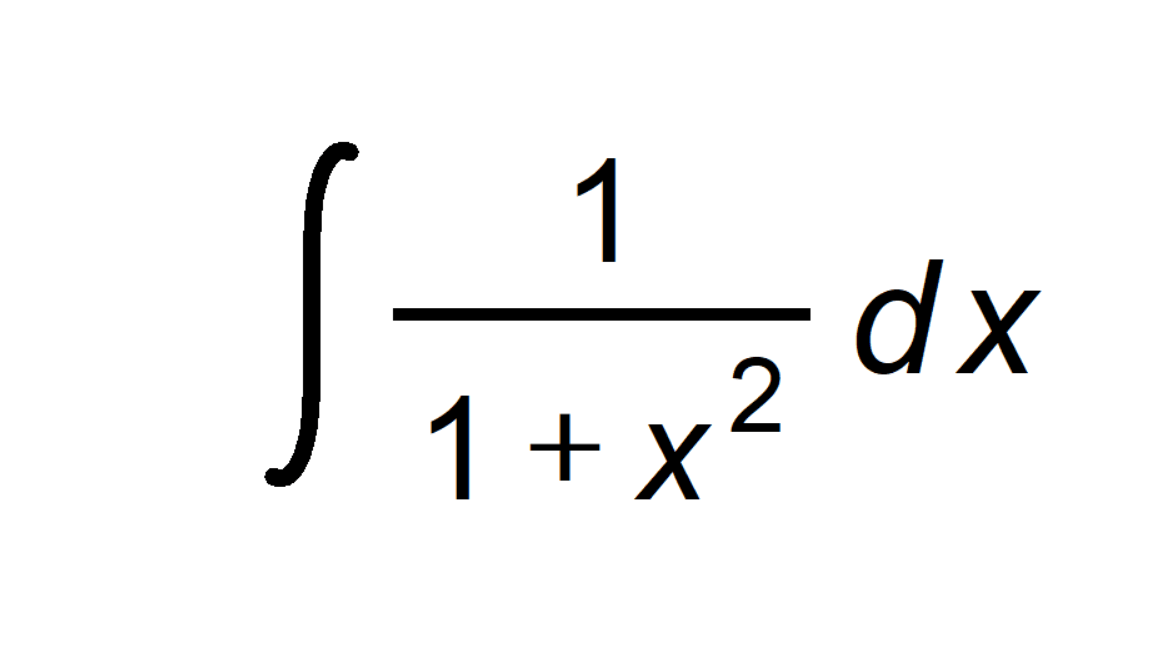Introduction: The antiderivative of 1/(1 + x²) is a classic problem in calculus. It’s a beautiful expression with deep connections to geometry and trigonometry. Let’s dive into the solution!

Step 1: Recognize the Expression

The given expression is the derivative of the arctangent function: ∫ 1/(1 + x²) dx

Step 2: Apply the Arctangent Integral

The integral of 1/(1 + x²) is the arctangent function: ∫ 1/(1 + x²) dx = arctan(x) + C

Conclusion: The antiderivative of 1/(1 + x²) is arctan(x) + C. This result is a cornerstone in calculus and has applications in various scientific fields. Mastering this integral equips you with a powerful mathematical tool!