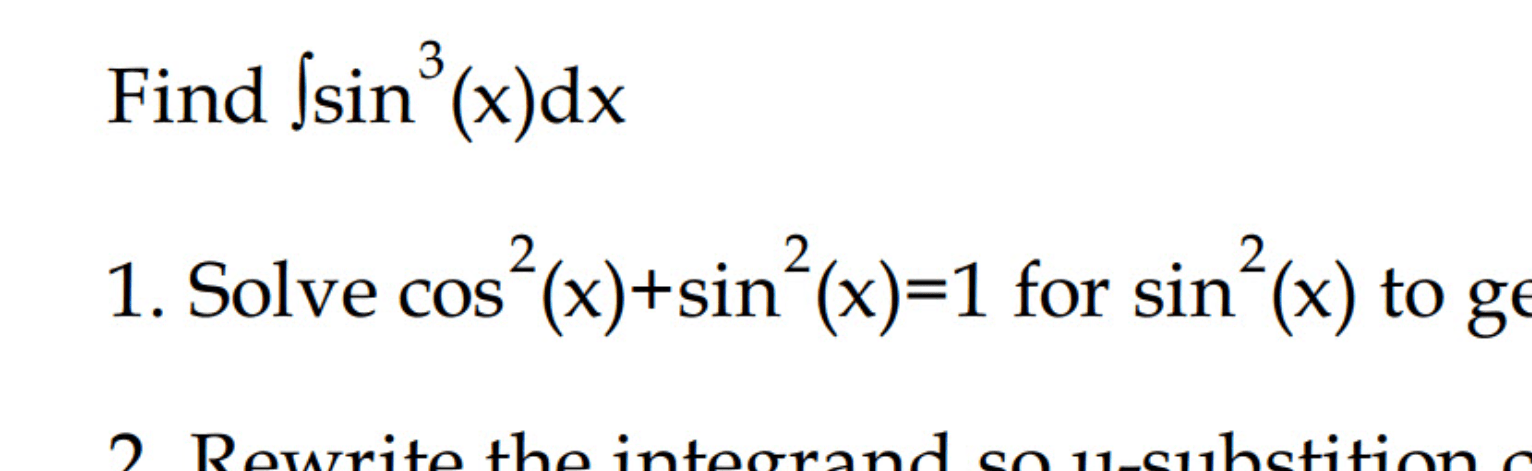Original Question: Find the integral of sin³(x).

1. Rewrite sin³(x) as a product of sin(x) and sin²(x):

sin³(x) = sin(x) ⋅ (1 – cos²(x))

We express sin³(x) as a product to make it easier to work with in the integral.

2. Make a substitution with u = cos(x):

du = -sin(x) dx

dx = du / (-sin(x))

We choose this substitution to simplify the expression inside the integral, as it will allow us to cancel out sin(x).

3. Substitute into the integral using the above expressions:

∫ sin³(x) dx = ∫ sin(x) ⋅ (1 – u²) ⋅ du / (-1)

By substituting our expressions for sin³(x) and dx, we can simplify the integral into a more manageable form.

4. Simplify the integral by canceling sin(x):

-∫ (1 – u²) du

We cancel sin(x) from the numerator and denominator, and we’re left with a simple polynomial integral.

5. Integrate the polynomial:

-u + u³ / 3 + C

We integrate the polynomial by finding the antiderivative of each term.

6. Substitute back for u using u = cos(x):

-cos(x) + cos³(x) / 3 + C

We replace u with cos(x) to express the final result in terms of the original variable x.