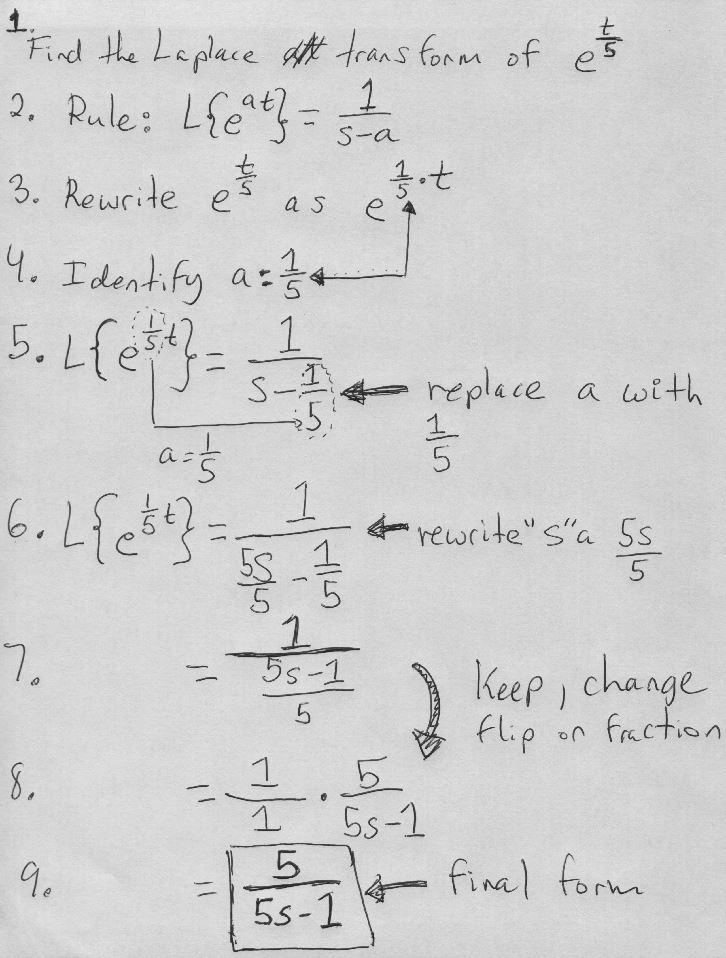
Detailed Steps for Finding the Laplace Transform of \( e^{t/5} \)

This guide offers an in-depth explanation of how to find the Laplace transform of \( e^{t/5} \), breaking down each step for better understanding.

Definition of Laplace Transform

The Laplace transform of a function \( f(t) \) is given by:

\[ \mathcal{L}\{ f(t) \} = \int_{0}^{\infty} e^{-st} f(t) \, dt \]

Step-by-Step Calculation

1. Start with the function \( f(t) = e^{t/5} \).

2. Substitute \( f(t) \) into the Laplace integral:

\[ \mathcal{L}\{ e^{t/5} \} = \int_{0}^{\infty} e^{-st} e^{t/5} \, dt \]

3. Combine the exponents:

\[ = \int_{0}^{\infty} e^{t(1/5 – s)} \, dt \]

4. Integrate with respect to \( t \):

\[ = \left[ \frac{1}{1/5 – s} e^{t(1/5 – s)} \right]_{0}^{\infty} \]

5. Evaluate the integral:

\[ = \frac{1}{s – 1/5} \]

Graph of the Laplace Transform

The graph below shows the Laplace transform of \( e^{t/5} \), which is \( \frac{1}{s – 1/5} \).

Conclusion

We’ve broken down each tiny step involved in finding the Laplace transform of \( e^{t/5} \). The graph provides a visual representation of this transform, aiding in understanding its behavior in the frequency domain.

Understanding Time and Frequency Domains via Laplace Transform

This guide aims to clarify how the Laplace transform allows us to switch between the time and frequency domains, facilitating easier analysis and problem-solving.

Time Domain

In the time domain, we deal with signals or functions of time, usually denoted as \( f(t) \). These functions describe how a particular quantity changes over time.

Frequency Domain

The frequency domain provides a different perspective, allowing us to analyze signals in terms of their frequency components. The Laplace transform converts a time-domain function \( f(t) \) into a frequency-domain function \( F(s) \).

The Laplace Transform

The Laplace transform is a mathematical tool that transforms a function from the time domain to the frequency domain using the following integral:

\[ \mathcal{L}\{ f(t) \} = \int_{0}^{\infty} e^{-st} f(t) \, dt \]

Interpreting the Transform

Once in the frequency domain, features like vertical asymptotes can provide insights into the behavior of the original time-domain function. For example, a vertical asymptote at \( s = 1/5 \) in the Laplace transform of \( e^{t/5} \) indicates an exponential growth rate in the original function.

Inverse Laplace Transform

The inverse Laplace transform allows us to go back from the frequency domain to the time domain, effectively reconstructing \( f(t) \) from \( F(s) \).

Conclusion

By understanding how to switch between the time and frequency domains using the Laplace transform, we can more easily analyze and solve complex problems, especially in fields like engineering and physics.