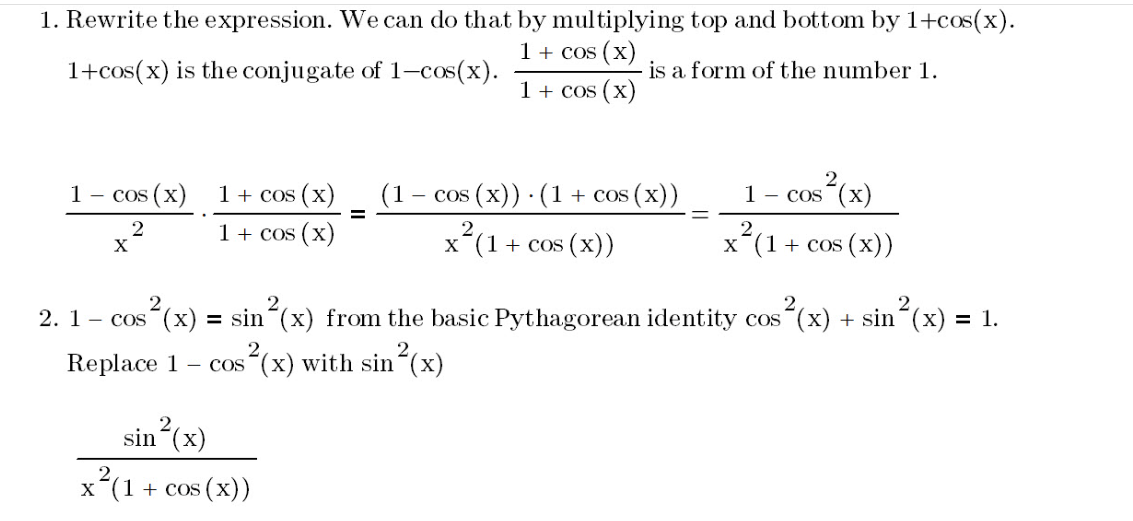Learn how to find the limit of (1-cos(x))/x² as x approaches 0 without L’Hôpital’s Rule. The result is ½ using standard trigonometric methods.
| Step |
Expression |
Explanation |
| 1 |
lim(x → 0) (1 – cos(x)) / x² |
Start with the original limit |
| 2 |
1 – cos(0) = 1 – 1 = 0 |
Plug in x = 0 into the numerator and simplify |
| 3 |
x² at x = 0 is 0 |
Plug in x = 0 into the denominator and simplify |
| 4 |
0 / 0 |
Check the form of the limit, which is indeterminate |
| 5 |
Multiply by (1 + cos(x)) / (1 + cos(x)) |
Rationalize the numerator |
| 6 |
(1 – cos(x)) * (1 + cos(x)) |
Expand the numerator part 1 |
| 7 |
(1 – cos²(x)) |
Expand the numerator part 2 |
| 8 |
sin²(x) / x²(1 + cos(x)) |
Use the trigonometric identity 1 – cos²(x) = sin²(x) |
| 9 |
(sin(x) / x)²(1 + cos(x)) |
Rewrite as a square of a known limit |
| 10 |
lim(x → 0) sin(x) / x = 1 |
Recall the known limit of sin(x) / x as x approaches 0 |
| 11 |
lim(x → 0) 1 + cos(x) = 1 + 1 = 2 |
Find the limit of 1 + cos(x) as x approaches 0 |
| 12 |
1² * 2 = 2 |
Plug in the known limits to find the overall limit is 2 |