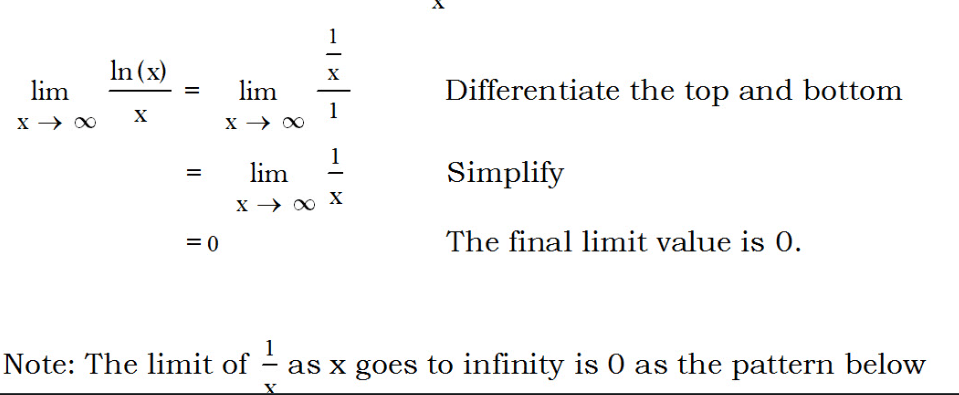Find the limit of ln(x)/x as x approaches infinity. Using calculus, the result is 0, a key concept in mathematical analysis.
Step Expression Explanation
1 lim(x → ∞) ln(x) / x Start with the original limit
2 ln(∞) = ∞, x = ∞ Plug in x = ∞ into the numerator and the denominator
3 ∞ / ∞ Check the form of the limit, which is indeterminate
4 Apply L’Hôpital’s Rule Since the limit is indeterminate, L’Hôpital’s Rule can be applied
5 d/dx ln(x) = 1/x Take the derivative of the numerator
6 d/dx x = 1 Take the derivative of the denominator
7 lim(x → ∞) 1/x / 1 Apply the derivatives to the limit
8 lim(x → ∞) 1/x = 0 Find the new limit
9 The limit is 0 The limit of the original expression is 0

limit of ln(x)/x as x goes to infinity