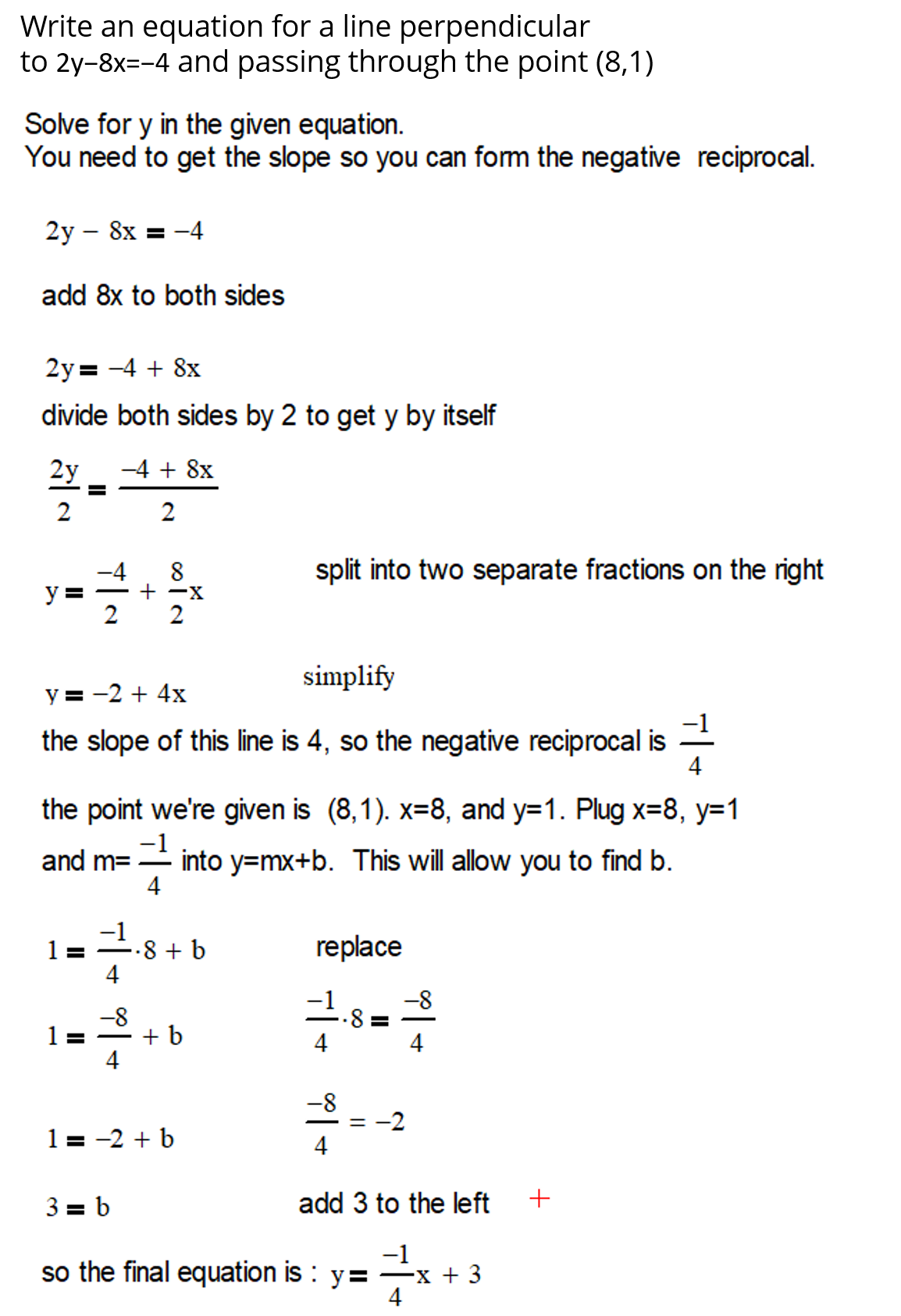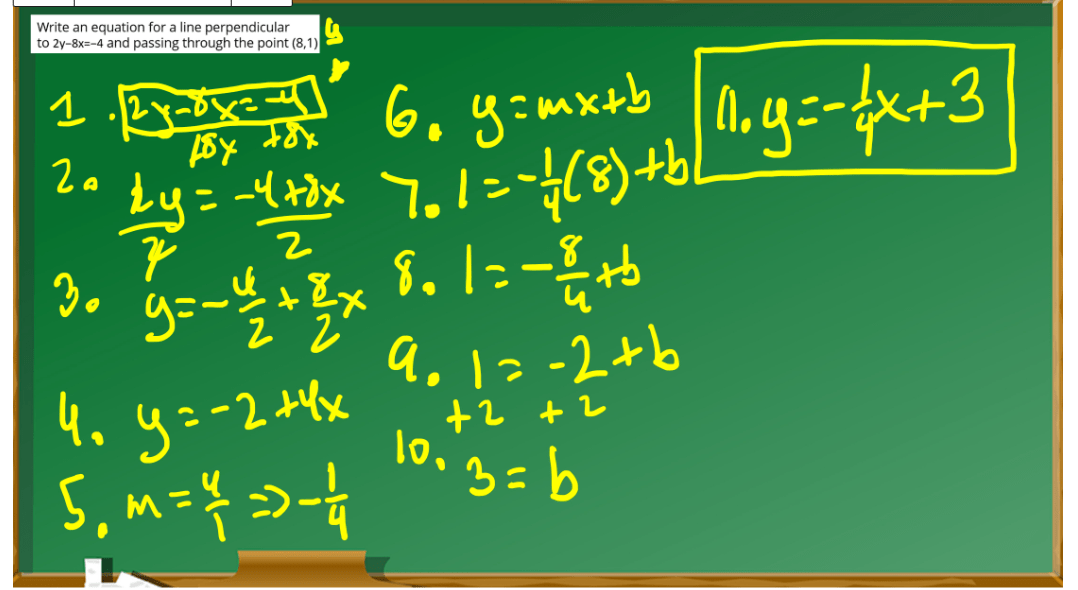Find the Equation of a Line Perpendicular to 2y – 8x = -4 at (8, 1)
Step 1: Find the Slope of the Given Line
The equation 2y – 8x = -4 can be rewritten in slope-intercept form y = mx + b as y = 4x + 2. The slope m of this line is 4.
Step 2: Find the Slope of the Perpendicular Line
The slope of a line perpendicular to a line with slope m is -1/m. For a slope of 4, the perpendicular slope is -1/4.
Step 3: Use Point-Slope Form to Find the Equation
The point-slope form of a line is y – y₁ = m(x – x₁), where m is the slope and (x₁, y₁) is a point on the line. Using the point (8, 1) and the perpendicular slope -1/4, the equation becomes y – 1 = -1/4(x – 8).
Step 4: Simplify the Equation
Distribute the -1/4 to get y – 1 = -1/4x + 2. Add 1 to both sides to get y = -1/4x + 3.
Summary
The equation of the line that is perpendicular to 2y – 8x = -4 and passes through the point (8, 1) is y = -1/4x + 3.
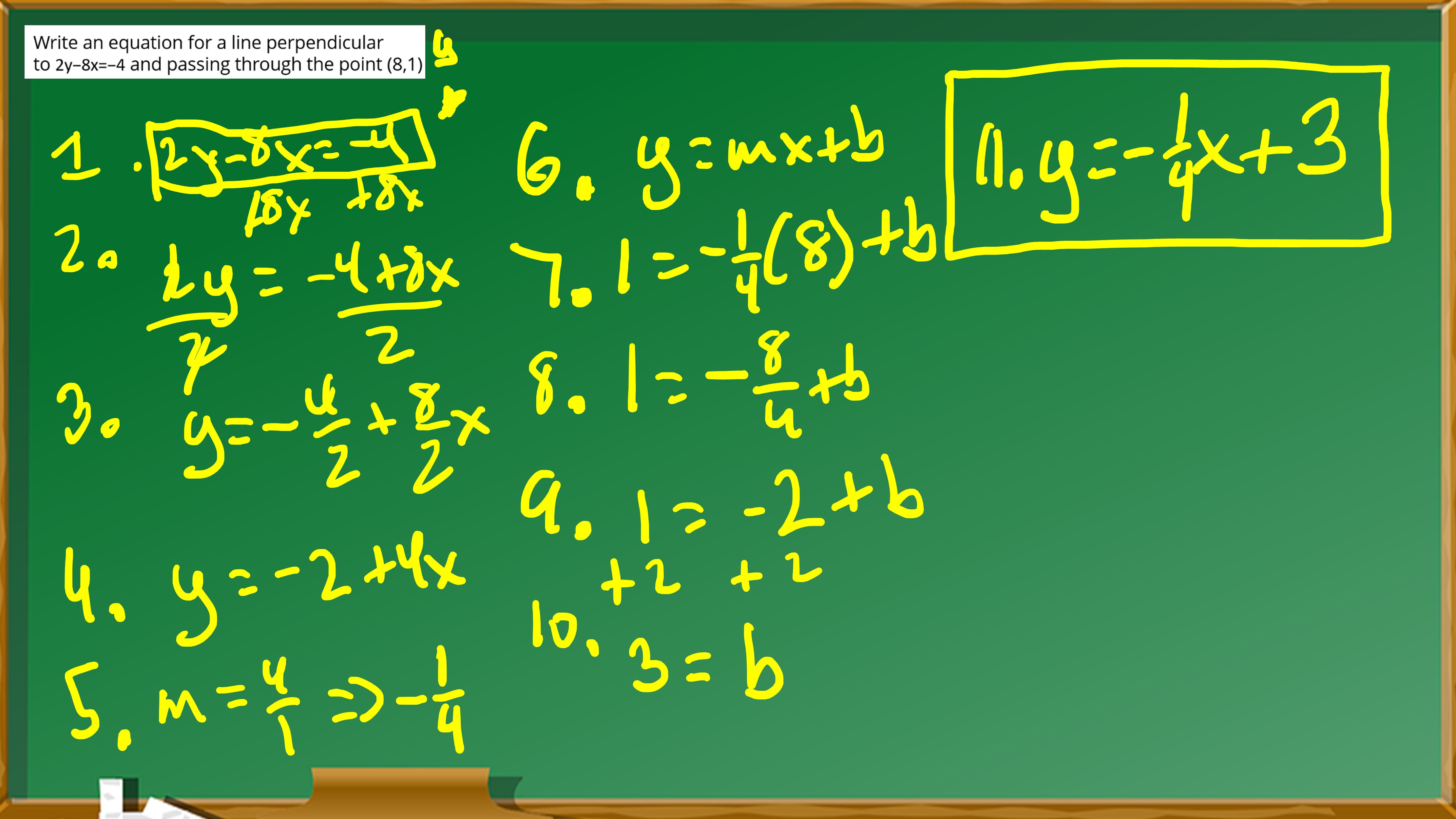
assignment 13, question 3