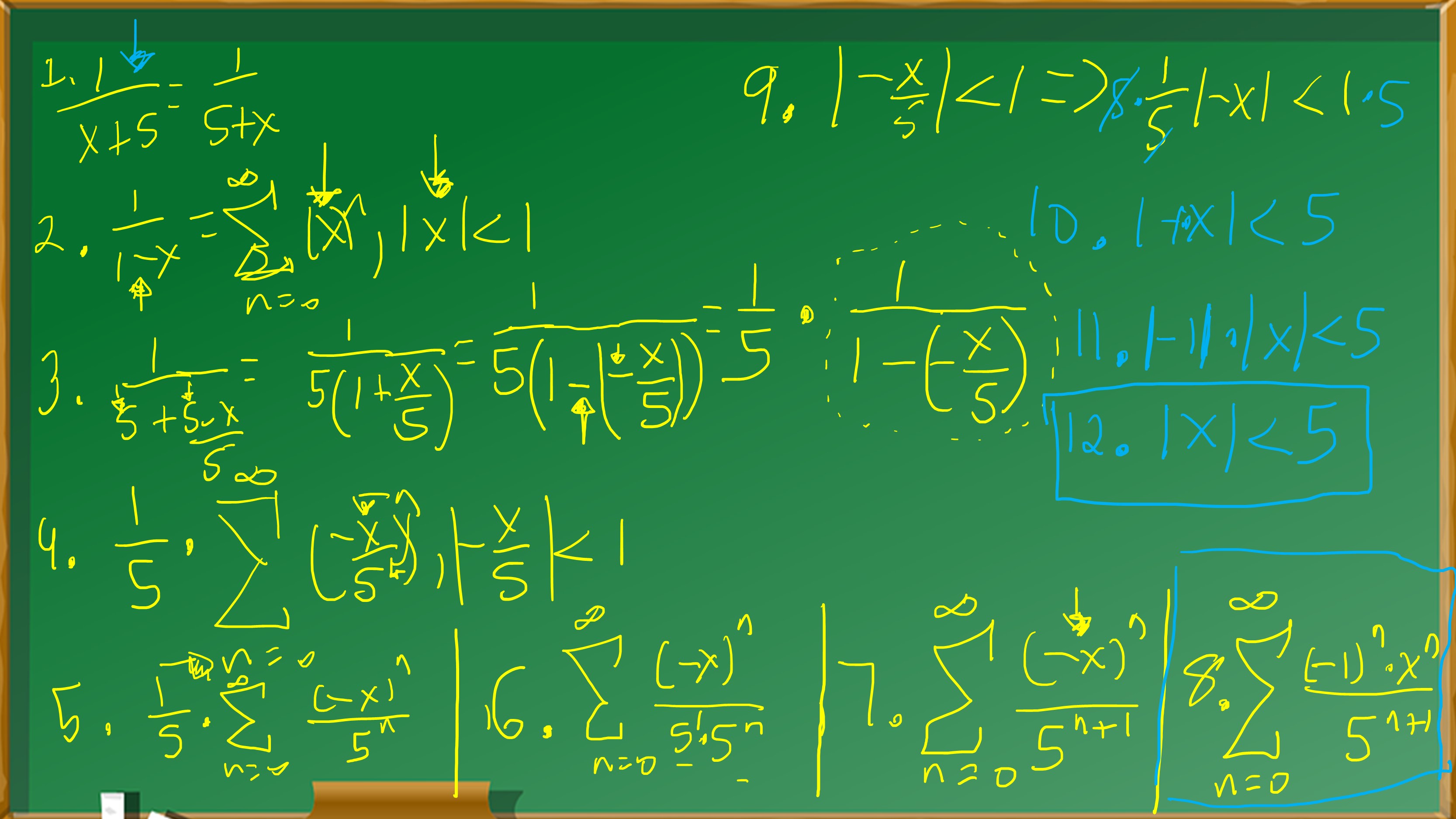
Step 1: Identifying the Function

We start with the function \( \frac{1}{5+x} \). Our objective is to find its series representation.

Step 2: Preparing for Series Expansion

Before we can expand the function into a series, we need to rewrite it in a form amenable to series expansion. Specifically, we aim to rewrite it in the form \( \frac{1}{1 – r} \).

Step 2.1: Isolating the Constant Term

First, we isolate the constant term ‘5’ in the denominator:

\[ \frac{1}{5+x} = \frac{1}{5} \times \frac{1}{1 + \frac{x}{5}} \]

Step 2.2: Identifying the Common Ratio \( r \)

Here, we identify \( r \) as \( -\frac{x}{5} \). This allows us to rewrite the function as:

\[ \frac{1}{1 + \frac{x}{5}} = \frac{1}{1 – (-\frac{x}{5})} \]

Step 3: Applying the Geometric Series Formula

Now that we have identified \( r \), we can use the geometric series formula \( 1 + r + r^2 + r^3 + \ldots \) to expand the function.

Step 3.1: Initial Expansion

We initially expand the function using the geometric series formula:

\[ \frac{1}{5} \times (1 – \frac{x}{5} + \left(\frac{x}{5}\right)^2 – \left(\frac{x}{5}\right)^3 + \ldots) \]

Step 4: Simplifying the Series

Each term in the series is simplified to make it easier to read and apply:

\[ \frac{1}{5} – \frac{x}{25} + \frac{x^2}{125} – \frac{x^3}{625} + \ldots \]

Step 5: Final Result

After all the steps, we arrive at the series representation for \( \frac{1}{5+x} \), which is \( \frac{1}{5} – \frac{x}{25} + \frac{x^2}{125} – \frac{x^3}{625} + \ldots \). This series is valid for \( |x| < 5 \).