Discover how to simplify complex mathematical expressions using power series. In this guide, we focus on the expression 1 / (1 + x²). We’ll walk you through each step to transform this expression into an infinite sum using the geometric series approach. By the end, you’ll understand how to represent 1 / (1 + x²) as the sum from n=0 to infinity of (-1)ⁿ xⁿ.

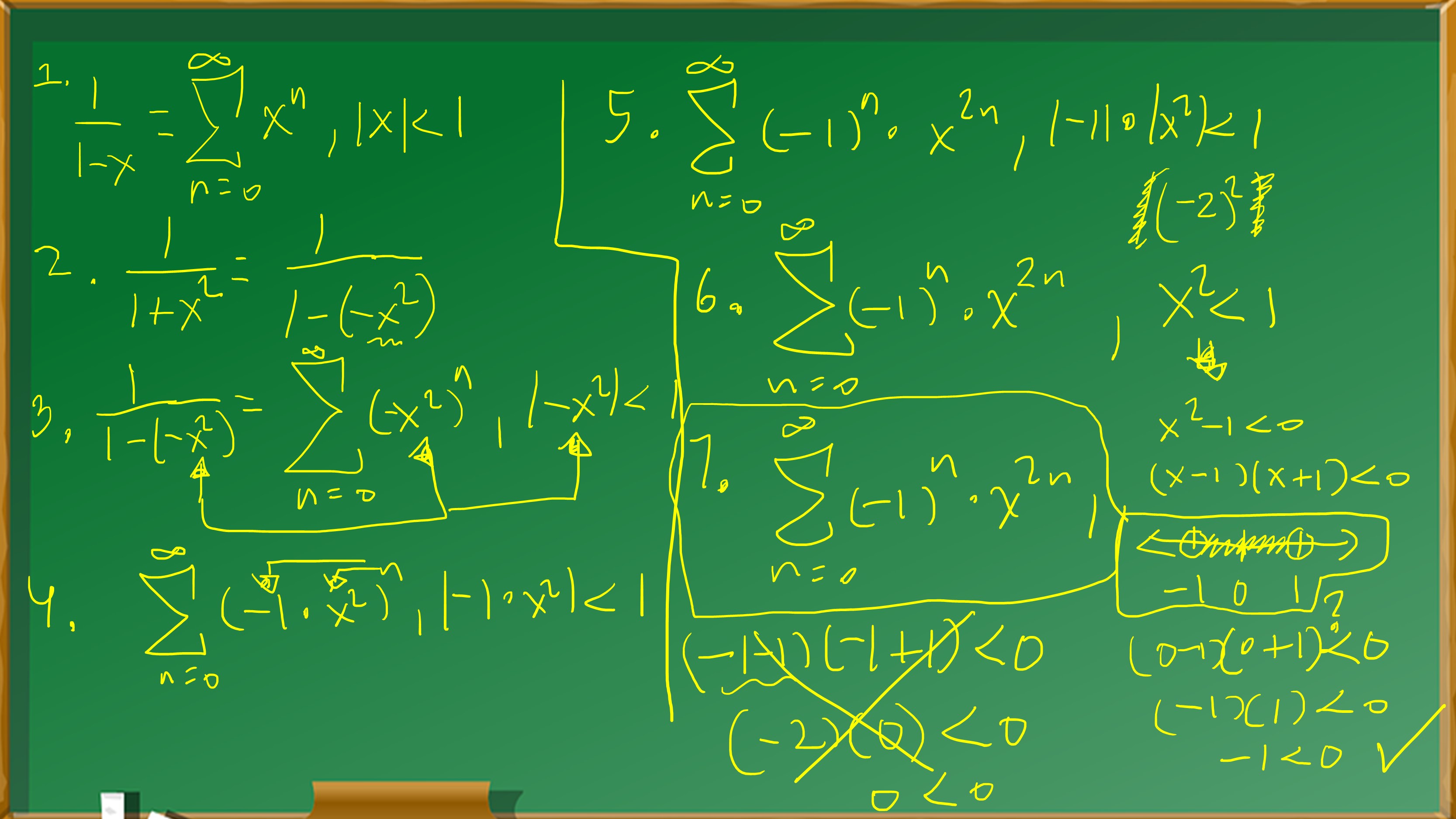
powerseriesfor1over1plusxsquared

 

Finding the Power Series for \( \frac{1}{1+x^2} \) Using the Geometric Series Approach

Math Step Explanation
\( \frac{1}{1+x^2} \) Start with the original expression.
\( \frac{1}{1 – (-x^2)} \) Rewrite the expression to fit the geometric series formula.
\( \sum_{n=0}^{\infty} (-x^2)^n \) Apply the geometric series formula to the expression.
\( \sum_{n=0}^{\infty} (-1)^n x^{2n} \) Simplify the series.

Summary

The power series representation for \( \frac{1}{1+x^2} \) using the geometric series approach is \( \sum_{n=0}^{\infty} (-1)^n x^{2n} \).