Rewriting 0.78 in Powers of 10

To rewrite the number 0.78 in terms of powers of 10, we break it down into its individual digits and multiply each by the appropriate power of 10:

0.78 = 7 × 10⁻¹ + 8 × 10⁻²

Why This Breakdown?

The breakdown is based on the place value system in decimal (base-10) numbers. In the number 0.78, each digit occupies a specific place:

• The digit 7 is in the tenths place, which corresponds to 10⁻¹.
• The digit 8 is in the hundredths place, which corresponds to 10⁻².

By multiplying each digit by the power of 10 that corresponds to its place and then summing these products, we can rewrite the number in terms of powers of 10.

Final Result

So, 0.78 can be rewritten as 7 × 10⁻¹ + 8 × 10⁻².

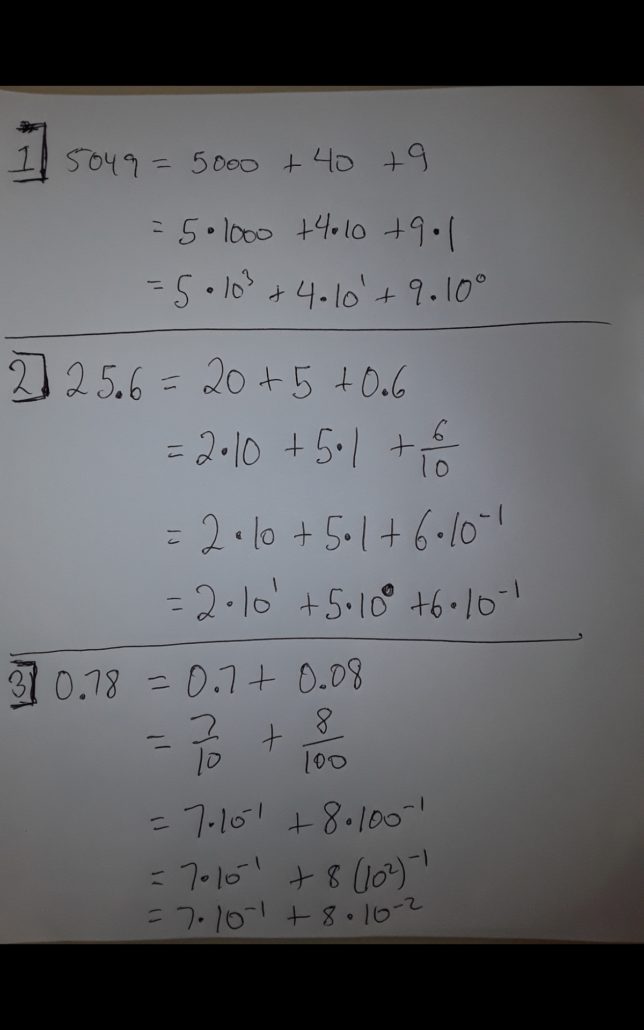
Rewriting 5049 in Powers of 10

To rewrite the number 5049 in terms of powers of 10, we break it down into its individual digits and multiply each by the appropriate power of 10:

5049 = 5 × 10³ + 0 × 10² + 4 × 10¹ + 9 × 10⁰

Why This Breakdown?

The breakdown is based on the place value system in decimal (base-10) numbers. In the number 5049, each digit occupies a specific place:

• The digit 5 is in the thousands place, which corresponds to 10³.
• The digit 0 is in the hundreds place, which corresponds to 10².
• The digit 4 is in the tens place, which corresponds to 10¹.
• The digit 9 is in the ones place, which corresponds to 10⁰.

By multiplying each digit by the power of 10 that corresponds to its place and then summing these products, we can rewrite the number in terms of powers of 10.

Final Result

So, 5049 can be rewritten as 5 × 10³ + 0 × 10² + 4 × 10¹ + 9 × 10⁰.

Rewriting 25.6 in Powers of 10

To rewrite the number 25.6 in terms of powers of 10, we break it down into its individual digits and multiply each by the appropriate power of 10:

25.6 = 2 × 10¹ + 5 × 10⁰ + 6 × 10⁻¹

Why This Breakdown?

The breakdown is based on the place value system in decimal (base-10) numbers. In the number 25.6, each digit occupies a specific place:

• The digit 2 is in the tens place, which corresponds to 10¹.
• The digit 5 is in the ones place, which corresponds to 10⁰.
• The digit 6 is in the tenths place, which corresponds to 10⁻¹.

By multiplying each digit by the power of 10 that corresponds to its place and then summing these products, we can rewrite the number in terms of powers of 10.

Final Result

So, 25.6 can be rewritten as 2 × 10¹ + 5 × 10⁰ + 6 × 10⁻¹.