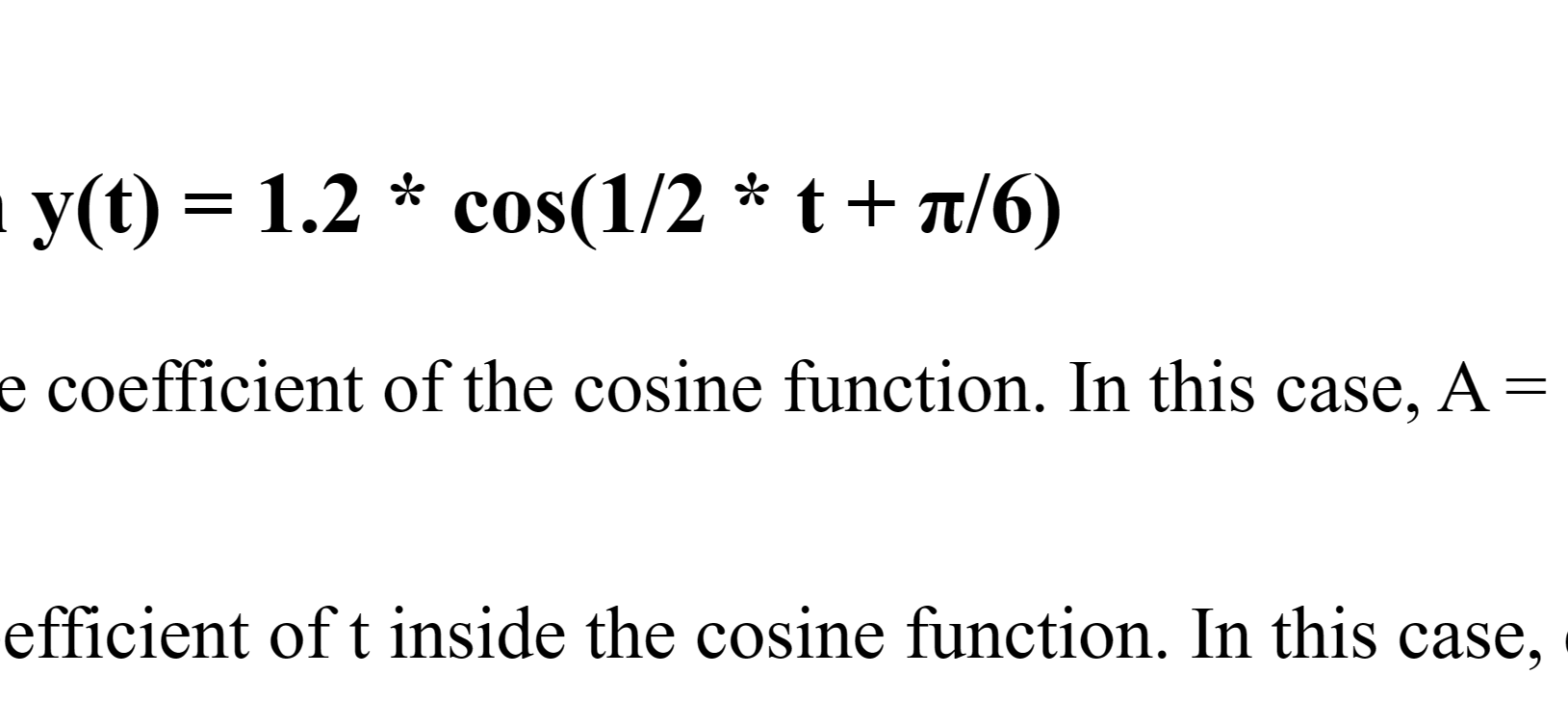Analyzing Trigonometric Cosine Functions: Amplitude, Frequency, Phase Shift, and Period
This section provides detailed analyses of three different examples of trigonometric cosine functions. Each analysis breaks down the amplitude, angular frequency, frequency, phase shift, and period of the function, providing a comprehensive understanding of these essential components.
Analysis of the Trigonometric Cosine Function y(t) = 1.2 * cos(1/2 * t + π/6)
Amplitude (A): The amplitude is the absolute value of the coefficient of the cosine function. In this case, A = |1.2| = 1.2. The units could be centimeters or meters.
Angular Frequency (ω): The angular frequency is the coefficient of t inside the cosine function. In this case, ω = 1/2 radians per second. It represents how quickly the function oscillates.
Frequency (f): The frequency is the angular frequency divided by 2 * π. In this case, f = (1/2) / (2 * π) = 1/(4 * π) ≈ 0.0796 cycles/second. It represents how many cycles occur in one second.
Phase Shift (δ): The phase shift is the constant added inside the cosine function. In this case, δ = -π/6 radians. It represents a horizontal shift in the graph of the function.
Period (T): The period is the reciprocal of the frequency. In this case, T = 1 / (1/(4 * π)) = 4 * π ≈ 12.566 seconds. It represents the time taken for one complete cycle of the function.
Conclusion: This detailed analysis of the trigonometric cosine function y(t) = 1.2 * cos(1/2 * t + π/6) breaks down every aspect of the function, including the amplitude, angular frequency, frequency, phase shift, and period. Understanding these properties is essential for a deep understanding of the trigonometric cosine function in various applications, and this analysis provides a step-by-step guide to each component.
Analysis of the Trigonometric Cosine Function y(t) = 2 * cos(3 * t – π/4)
Amplitude (A): The amplitude is the absolute value of the coefficient of the cosine function. In this case, A = |2| = 2. The units could be centimeters or meters.
Angular Frequency (ω): The angular frequency is the coefficient of t inside the cosine function. In this case, ω = 3 radians per second. It represents how quickly the function oscillates.
Frequency (f): The frequency is the angular frequency divided by 2 * π. In this case, f = 3 / (2 * π) ≈ 0.4775 cycles/second. It represents how many cycles occur in one second.
Phase Shift (δ): The phase shift is the constant subtracted inside the cosine function. In this case, δ = π/4 radians. It represents a horizontal shift in the graph of the function.
Period (T): The period is the reciprocal of the frequency. In this case, T = 1 / (3 / (2 * π)) = 2 * π / 3 ≈ 2.094 seconds. It represents the time taken for one complete cycle of the function.
Conclusion: This detailed analysis of the trigonometric cosine function y(t) = 2 * cos(3 * t – π/4) breaks down every aspect of the function, including the amplitude, angular frequency, frequency, phase shift, and period. Understanding these properties is essential for a deep understanding of the trigonometric cosine function in various applications, and this analysis provides a step-by-step guide to each component.
Analysis of the Trigonometric Cosine Function y(t) = 0.5 * cos(4 * t + π/3)
Amplitude (A): The amplitude is the absolute value of the coefficient of the cosine function. In this case, A = |0.5| = 0.5. The units could be centimeters or meters.
Angular Frequency (ω): The angular frequency is the coefficient of t inside the cosine function. In this case, ω = 4 radians per second. It represents how quickly the function oscillates.
Frequency (f): The frequency is the angular frequency divided by 2 * π. In this case, f = 4 / (2 * π) ≈ 0.6366 cycles/second. It represents how many cycles occur in one second.
Phase Shift (δ): The phase shift is the constant added inside the cosine function. In this case, δ = -π/3 radians. It represents a horizontal shift in the graph of the function.
Period (T): The period is the reciprocal of the frequency. In this case, T = 1 / (4 / (2 * π)) = π / 2 ≈ 1.571 seconds. It represents the time taken for one complete cycle of the function.
Conclusion: This detailed analysis of the trigonometric cosine function y(t) = 0.5 * cos(4 * t + π/3) breaks down every aspect of the function, including the amplitude, angular frequency, frequency, phase shift, and period. Understanding these properties is essential for a deep understanding of the trigonometric cosine function in various applications, and this analysis provides a step-by-step guide to each component.