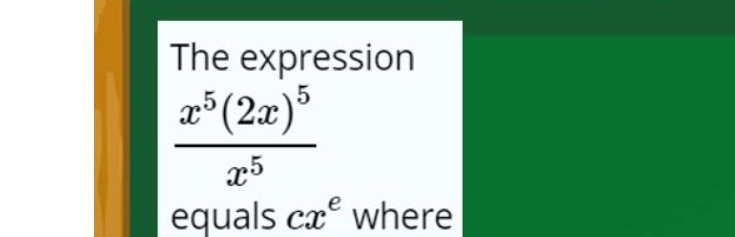Learn how to simplify complex mathematical expressions step-by-step. In this guide, we break down the expression (x⁵)(2x)⁵ / x⁵. We’ll walk you through each step, from expanding terms to combining and simplifying exponents, to help you understand how to arrive at the simplified expression, which is 32x⁵.

Simplifying the Expression \( \frac{(x^5)(2x)^5}{x^5} \)
| Math Step | Explanation |
|---|---|
| \( \frac{(x^5)(2x)^5}{x^5} \) | Start with the original expression. |
| \( \frac{(x^5)(32x^5)}{x^5} \) | Expand \( (2x)^5 \) to \( 32x^5 \). |
| \( \frac{32x^{5+5}}{x^5} \) | Combine the exponents in the numerator by writing them as \( 5+5 \). |
| \( \frac{32x^{10}}{x^5} \) | Simplify the exponent in the numerator by adding 5 and 5, resulting in \( 32x^{10} \). |
| \( 32x^{10-5} \) | Divide the exponents by writing them as \( 10-5 \). |
| \( 32x^5 \) | Simplify the exponent by subtracting 5 from 10, resulting in \( 32x^5 \). |
Summary
The simplified expression is \( 32x^5 \).