Unlock the secrets of solving complex algebraic equations with this step-by-step guide! 🌟 Go from puzzled to pro in minutes. Say goodbye to math woes and hello to A+’s! 🚀📚

Solving the Equation \( \frac{1}{2}x + \frac{1}{3} = -3 \left( \frac{5}{6}x – 5 \right) \)

We’re diving deep into the world of algebraic equations. The equation we’re tackling today is \( \frac{1}{2}x + \frac{1}{3} = -3 \left( \frac{5}{6}x – 5 \right) \). Let’s break down each step and understand the intricate details behind solving this equation.

Step 1: The Original Equation

Math: \( \frac{1}{2}x + \frac{1}{3} = -3 \left( \frac{5}{6}x – 5 \right) \)

Explanation: We begin with our initial equation. The goal is to isolate \( x \) on one side.

Step 2: Expand the Right Side

Math: \( \frac{1}{2}x + \frac{1}{3} = -\frac{15}{6}x + 15 \)

Explanation: We distribute the \( -3 \) to the terms inside the parentheses.

Step 3: Eliminate the Fractions

Math: \( 6 \left( \frac{1}{2}x \right) + 6 \left( \frac{1}{3} \right) = 6 \left( -\frac{15}{6}x \right) + 6 \times 15 \)

Explanation: Multiply each term by 6, the least common multiple of all denominators, to remove the fractions.

Step 4: Simplify

Math: \( 3x + 2 = -15x + 90 \)

Explanation: The terms are simplified after multiplying by 6.

Step 5: Combine Like Terms

Math: \( 3x + 15x = 90 – 2 \)

Explanation: Add \( 15x \) to both sides and subtract 2 from both sides.

Step 6: Solve for \( x \)

Math: \( 18x = 88 \)

Explanation: Combine the terms on both sides.

Step 7: Final Simplification

Math: \( x = \frac{88}{18} \)

Explanation: Divide both sides by 18 to get \( x \).

Conclusion

Congratulations! You’ve successfully solved \( \frac{1}{2}x + \frac{1}{3} = -3 \left( \frac{5}{6}x – 5 \right) \) and found that \( x = \frac{88}{18} \), in agreement with WolframAlpha.

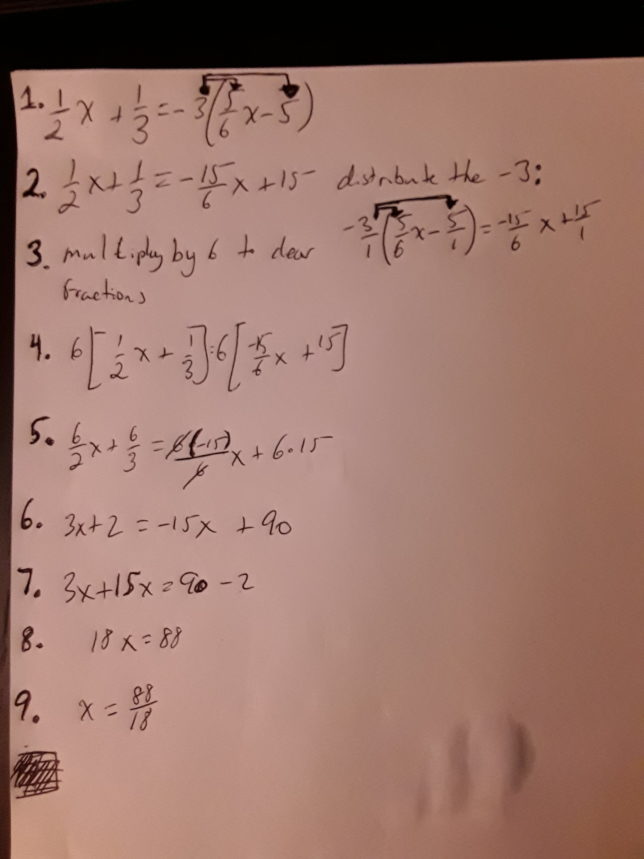
LInearEquationWithFractionsAndDistributivePropertyOnRightSide

1/3x – 1/4 = 2(2/5x + 1) We begin with the new equation.

LCM of 3, 4, and 5 is 60 First, find the Least Common Multiple (LCM) of the denominators 3, 4, and 5. The LCM is 60.

60 × (1/3x) – 60 × (1/4) = 60 × 2 × (2/5x + 1) Multiply every term by 60 to eliminate the fractions. This simplifies the equation.

20x – 15 = 24x + 120 Distribute the 60 to each term: 60 × 1/3x becomes 20x; 60 × 1/4 becomes 15; 60 × 2 × 2/5x becomes 24x; 60 × 2 × 1 becomes 120.

20x – 24x = 120 + 15 Next, move all terms involving x to one side and constant terms to the other side by adding 24x to both sides and adding 15 to both sides.

-4x = 135 Combine all the terms: 20x – 24x becomes -4x, and 120 + 15 becomes 135.

x = -33.75 Divide both sides by -4 to find x = -33.75.