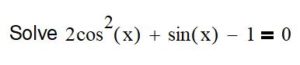Step	Comment
Step 1	Identify the equation, which is $2co{s}^2(x)+sin(x)–1=0$.
Step 2	Use the Pythagorean identity $si{n}^2(x)+co{s}^2(x)=1$ to express $co{s}^2(x)$ as $1–si{n}^2(x)$.
Step 3	Substitute $1–si{n}^2(x)$ for $co{s}^2(x)$ in the equation to get $2(1–si{n}^2(x))+sin(x)–1=0$.
Step 4	Simplify the equation to get $2–2si{n}^2(x)+sin(x)–1=0$.
Step 5	Further simplify the equation to get $2si{n}^2(x)–sin(x)–1=0$.
Step 6	This is a quadratic equation in terms of $sin(x)$. We can solve it by factoring: $2si{n}^2(x)–sin(x)–1=0$ factors to $(2sin(x)+1)(sin(x)–1)=0$.
Step 7	Set each factor equal to zero and solve for $sin(x)$ to get $sin(x)=-1/2$ or $sin(x)=1$.
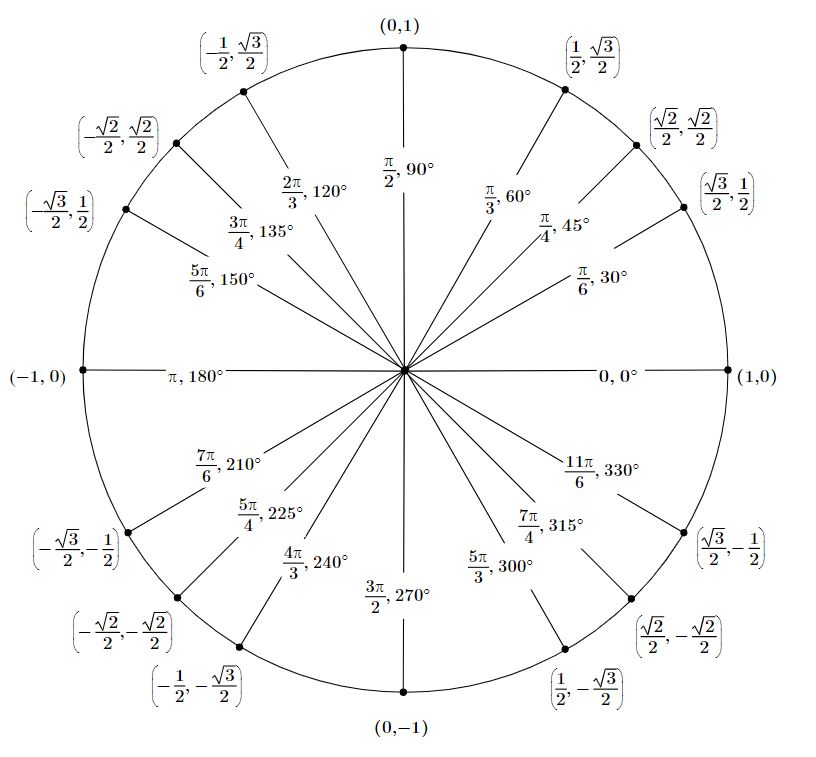
Step 8	Find the values of $x$ that satisfy $sin(x)=-1/2$. These are $x=7\pi /6,11\pi /6$.
Step 9	Find the values of $x$ that satisfy $sin(x)=1$. This is $x=\pi /2$.
Step 10	Note that these are the solutions in the first period $[0,2\pi )$. The general solutions can be found by adding $2\pi n$ to each of these solutions, where $n$ is an integer.

---