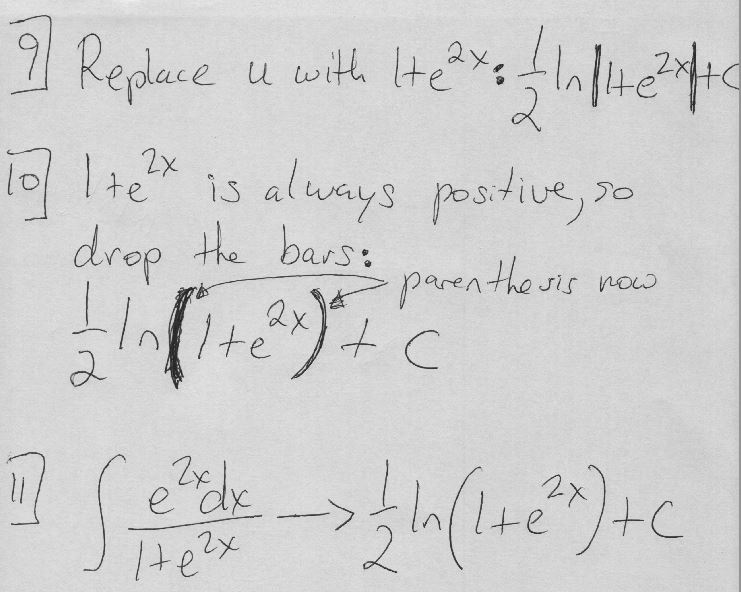
Integral of \( \frac{e^{2x}}{1 + e^{2x}} \)

In calculus, the integral of a function provides the area under the curve of that function. Here, we are interested in finding the integral of \( \frac{e^{2x}}{1 + e^{2x}} \), a function that involves exponential terms. This is a common type of problem in integral calculus, often requiring substitution methods for solving.

Step-by-Step Solution

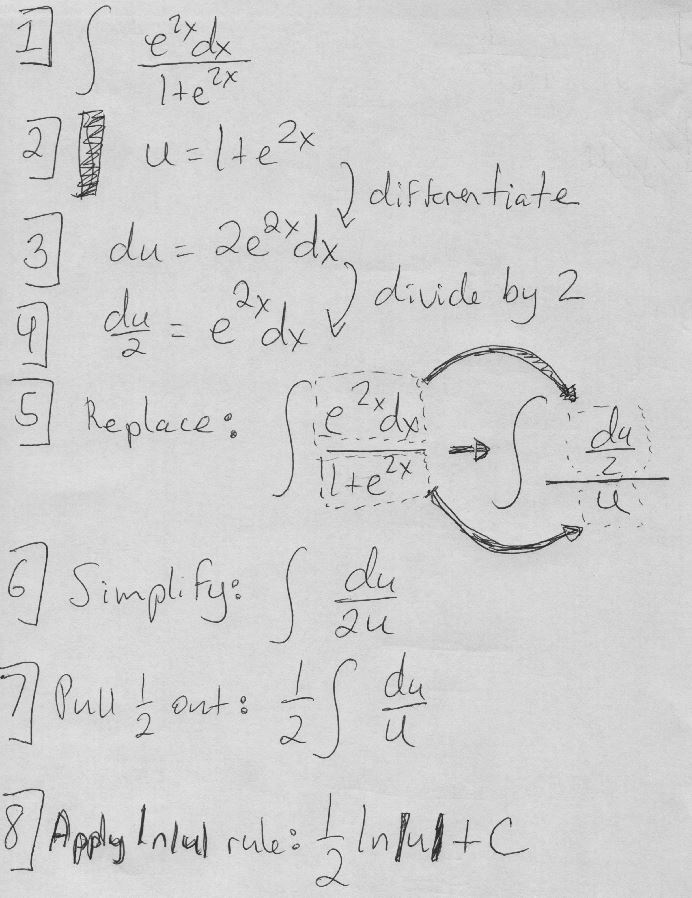
Step 1: Substitution
We start by making a substitution to simplify the integral. Let \( u = 1 + e^{2x} \). The differential \( du = 2 e^{2x} dx \), and \( e^{2x} dx = \frac{du}{2} \).

Step 2: Rewrite the Integral in terms of \( u \)
The integral becomes \( \frac{1}{2} \int \frac{du}{u} \).

Step 3: Integrate
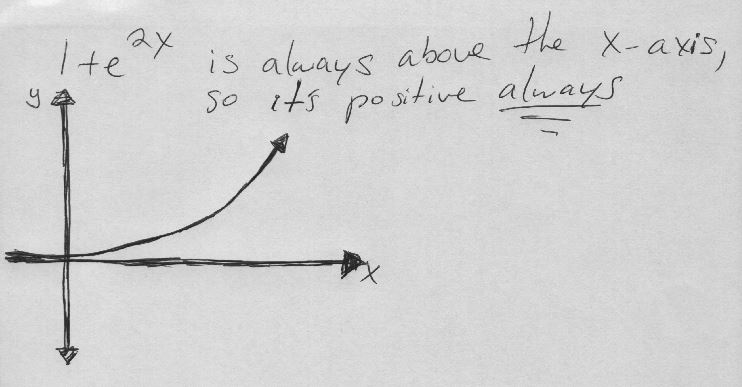
The integral of \( \frac{1}{u} \) is \( \ln|u| \). Since \( u = 1 + e^{2x} \) is always positive, we can remove the absolute value bars, resulting in \( \frac{1}{2} \ln(u) + C \).

Step 4: Back-Substitute
Finally, we back-substitute \( u = 1 + e^{2x} \) to get the integral \( \frac{1}{2} \ln(1 + e^{2x}) + C \).

This integral is particularly useful in problems involving exponential growth and decay, and it’s a great example of how substitution can simplify a complex-looking integral. The removal of the absolute value bars is justified because \( 1 + e^{2x} \) is always positive.