Given:
In this geometry problem, we are given the points C(-2, -1), D(5, -4), and Q(4, 2). The goal is to find a location for a point P(x, y) such that the line segment PQ is perpendicular to the line segment CD.
Solution:
1. The first step is to calculate the slope of the segment CD. The slope of a line between two points is calculated using the formula:
(y₂ – y₁) / (x₂ – x₁)
For points C(-2, -1) and D(5, -4), this gives us the slope of CD as:
(-4 – (-1)) / (5 – (-2)) = -3 / 7
2. Since the line segment PQ is perpendicular to the line segment CD, we need the negative reciprocal of the slope of CD. The negative reciprocal of -3/7 is 7/3. This is the slope of line segment PQ.
3. Now, using the slope of PQ and the coordinates of point Q(4, 2), we set up the slope formula for the line PQ:
(2 – y) / (4 – x) = 7 / 3
4. To solve for the coordinates of point P(x, y), we equate the numerator and denominator on both sides of the equation. This gives us two simple linear equations:
4 – x = 3 and 2 – y = 7
Solving these equations gives:
x = 1 and y = -5
Final Answer:
The point P is (1, -5). This means that the point P(1, -5) satisfies the condition that line PQ is perpendicular to line CD.
Check:
To verify the solution, we substitute the coordinates of P(1, -5) back into the slope equation:
(2 – (-5)) / (4 – 1) = 7 / 3
Since both sides of the equation are equal, the solution is correct.
This step-by-step solution uses basic geometry and algebra to find the point P that makes the line segment PQ perpendicular to the line segment CD. The key concept here is understanding how to find the slope of a line and apply the perpendicularity condition using negative reciprocals. By solving for the unknowns x and y, we determined that the point P(1, -5) is the correct solution.
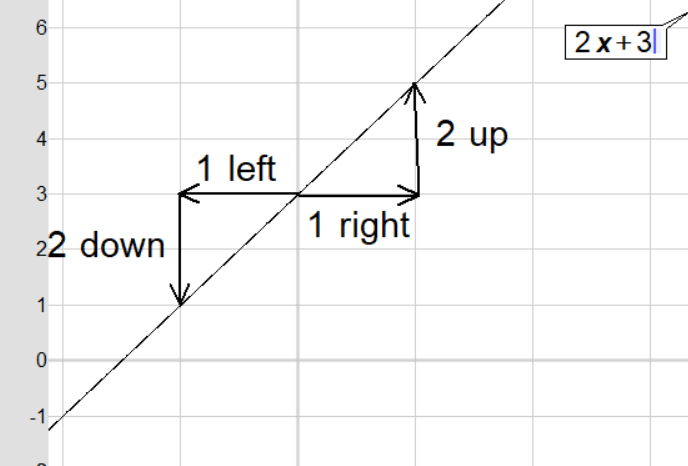
Explanation: Consider the line equation y = 2x + 3, which has a slope of 2. This means for every 1 unit moved to the right, the y-coordinate increases by 2 units.
Starting from the point (0, 3), which lies on the line (because substituting x = 0 into the equation gives y = 2(0) + 3 = 3), let’s first move 1 unit to the right. The x-coordinate changes from 0 to 1.
Substituting x = 1 into the line equation:
y = 2(1) + 3 = 2 + 3 = 5.
So, after moving 1 unit to the right and 2 units up, you arrive at the point (1, 5), which also lies on the line since it satisfies the equation y = 2x + 3.
Now, let’s check if moving in the opposite direction (1 unit left and 2 units down) also keeps us on the same line.
From (0, 3), if you move 1 unit to the left, the x-coordinate becomes -1. Substituting x = -1 into the equation:
y = 2(-1) + 3 = -2 + 3 = 1.
This gives the point (-1, 1), which also satisfies the equation y = 2x + 3 and lies on the same line.
Therefore, moving 1 unit left and 2 units down places you at a point that satisfies the line equation, keeping you on the same line. This shows that both movements (1 unit right and 2 units up or 1 unit left and 2 units down) follow the same line and keep you on it.
Question:
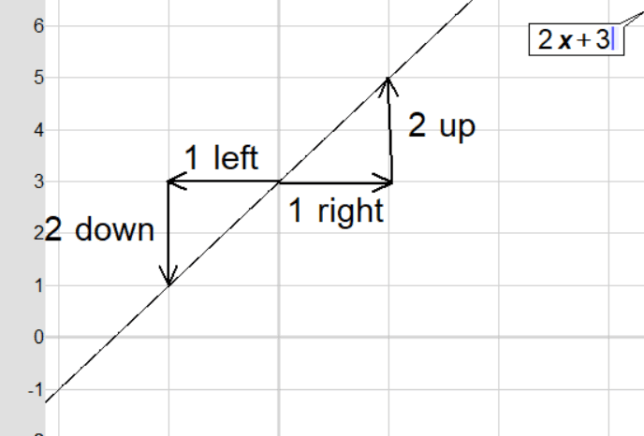
Given the function f(x) = 2^(0.5x) defined over [0, 2], what is the new domain of the function if x is replaced by 2x, resulting in g(x) = f(2x) = 2^x?
A. [0, 0.5]
B. [0, 1]
C. [0, 2]
Solution:
To find the new domain, we start with the inequality 0 ≤ 2x ≤ 2, which comes from the original domain [0, 2]. Dividing the entire inequality by 2, we get 0 ≤ x ≤ 1. Therefore, the new domain of g(x) is [0, 1].
Confirmation:
For the original function f(x) = 2^(0.5x), at x = 2, f(2) = 2^1 = 2. For the new function g(x) = 2^x, at x = 1, g(1) = 2^1 = 2. Thus, g(1) equals f(2).
Correct answer: B. [0, 1]
Question:
How much should be added to the 1 in the equation y = 2 / 1 * x + 3 to make the new line three times as steep as the given line?
Answer Choices:
- 2 / 3
- -2 / 3
- -1
Solution:
We want to make the new line three times as steep as the given line. The current slope is 2 / 1 = 2, and we want the new slope to be 6.
Let’s assume we need to add some value to the denominator. The new slope would be:
2 / (1 + a)
We want this new slope to equal 6:
2 / (1 + a) = 6
Now, solve for a:
First, multiply both sides by (1 + a):
2 = 6 * (1 + a)
Next, expand the right-hand side:
2 = 6 + 6a
Now subtract 6 from both sides:
-4 = 6a
Finally, divide both sides by 6:
a = -4 / 6 = -2 / 3
Since a = -2 / 3, we are adding -2 / 3 to 1. The negative sign indicates that we are effectively subtracting 2 / 3 from 1.
Thus, the correct answer is: -2 / 3.
Final Answer: -2 / 3
Question:
What fraction of a in the equation y = (b / a) * x + m should be added to a to make the slope twice b?
Granular Step-by-Step Solution:
1. Start with the given equation:
y = (b / a) * x + m
The current slope is the coefficient of x, which is (b / a). So the current slope is:
slope = b / a
2. The desired slope:
We want the slope to be twice b. This means the new slope should be:
slope = 2b
3. Adding a fraction of a:
Let f be the fraction of a that we are adding to a. The new denominator becomes:
a + f * a = a(1 + f)
So the new slope is:
slope = b / (a(1 + f))
4. Set up the equation:
We want the new slope to equal 2b, so we set the new slope equal to 2b:
b / (a(1 + f)) = 2b
5. Divide both sides by b:
Assuming b ≠ 0, divide both sides of the equation by b. This simplifies the equation to:
1 / (a(1 + f)) = 2
6. Multiply both sides by a(1 + f):
Next, multiply both sides by a(1 + f) to remove the fraction:
1 = 2 * a * (1 + f)
7. Divide by 2:
Divide both sides by 2 to start isolating f:
1 / 2 = a * (1 + f)
8. Solve for f:
Now divide both sides by a to isolate (1 + f):
1 / (2a) = 1 + f
9. Subtract 1 from both sides:
f = (1 / (2a)) – 1
10. Combine the terms:
To combine the terms, write 1 as (2a / 2a) so both terms have the same denominator:
f = (1 / (2a)) – (2a / (2a))
11. Simplify:
Now combine the terms over a common denominator:
f = (1 – 2a) / (2a)
Final Answer: The fraction of a that we need to add to a is (1 – 2a) / (2a).
Correct Verification Check:
Now let’s check if this value for f gives us the desired slope of 2b:
12. Use the value of f in the new slope formula:
The new denominator is a + f * a. Substituting f = (1 – 2a) / (2a) into this:
New denominator = a + ((1 – 2a) / (2a)) * a
13. Multiply out the expression:
((1 – 2a) / (2a)) * a = (1 – 2a) / 2
14. Add this to the original a:
New denominator = a + (1 – 2a) / 2
Rewrite a as 2a / 2 so we can add the terms:
New denominator = (2a / 2) + (1 – 2a) / 2
15. Combine the terms in the denominator:
New denominator = (2a + 1 – 2a) / 2 = 1 / 2
16. Recalculate the new slope:
The new slope is:
b / (1 / 2) = b * 2 = 2b
So, the new slope is indeed 2b, confirming that the solution is correct.
Given Equation:
1 / ∫ x dx + 4 = 56
Step 1: Isolate the integral term.
Subtract 4 from both sides:
1 / ∫ x dx = 56 – 4
1 / ∫ x dx = 52
Step 2: Solve for the integral of x.
Take the reciprocal of both sides:
∫ x dx = 1 / 52
Step 3: Evaluate the indefinite integral of x.
The integral of x is:
∫ x dx = (x²) / 2 + C
Substitute this back into the equation:
(x²) / 2 + C = 1 / 52
Step 4: Solve for x by iterating over C.
For C = -1:
(x²) / 2 – 1 = 1 / 52
Solve for x: x ≈ ±1.43
For C = 0:
(x²) / 2 = 1 / 52
Solve for x: x ≈ ±0.20
For C = 1:
(x²) / 2 + 1 = 1 / 52
Solve for x: x ≈ ±1.40i (imaginary value)
Conclusion:
The choice of C = 1 results in an imaginary value for x.
Question: A function made of segments goes from (0,0) to (1,1) and then to (3,7). What’s the domain of the inverse and the range of the inverse?
Answer Options:
- domain = [0,3], range = [0,7]
- domain = [0,7], range = [0,7]
- domain = [0,7], range = [0,3] (correct)
Explanation:
The function described consists of two segments:
- From (0, 0) to (1, 1)
- From (1, 1) to (3, 7)
Understanding the Function:
The domain of the original function is the set of all x-values that the function covers. For this function, the x-values range from 0 to 3 because:
- The first segment goes from x = 0 to x = 1.
- The second segment goes from x = 1 to x = 3.
Therefore, the domain of the original function is [0, 3].
The range of the original function is the set of all y-values that the function takes. From the segments provided, the y-values range from 0 to 7 because:
- The first segment goes from y = 0 to y = 1.
- The second segment goes from y = 1 to y = 7.
Therefore, the range of the original function is [0, 7].
Inverse of the Function:
The domain and range of the inverse function are swapped with respect to the original function.
- The domain of the inverse becomes the range of the original function, which is [0, 7].
- The range of the inverse becomes the domain of the original function, which is [0, 3].
Thus, the correct domain and range of the inverse function are:
- Domain: [0, 7]
- Range: [0, 3]
📘 Solution Explained
Problem:
Find the sum of:
1. The integral of x² from x = 0 to x = 2.
2. The integral of its inverse function over the appropriate domain.
Step 1: Integral of x² from 0 to 2
∫₀² x² dx = (x³)/3 │₀² = (2³)/3 – (0³)/3 = 8/3
Step 2: Integral of the Inverse Function
– Original Function: y = x² (x ≥ 0)
– Inverse Function: x = √y
– Domain for Inverse: When x = 0, y = 0; when x = 2, y = 4
∫₀⁴ √y dy = (2/3) y^(3/2) │₀⁴ = (2/3)(4)^(3/2) – (2/3)(0)^(3/2) = (2/3)(8) = 16/3
Step 3: Sum of Both Integrals
8/3 + 16/3 = 24/3 = 8
✅ Final Answer: 8
Quiz Question:
Consider the function f(x) = 1/(x + 5). What is f^(-1)(x) and its domain and range?
Answer Choices:
A) f^(-1)(x) = 1/x + 5; Domain: (-∞, ∞), Range: (-∞, ∞)
B) f^(-1)(x) = 1/x – 5; Domain: (-∞, 0) ∪ (0, ∞), Range: (-∞, -5) ∪ (-5, ∞)
C) f^(-1)(x) = x/(x-5); Domain: (-∞, 5) ∪ (5, ∞), Range: (-∞, ∞)
Solution:
Algebraic Method:
Given f(x) = 1/(x + 5)
y = 1/(x + 5) → x = 1/(y + 5) // Swap x and y
x(y + 5) = 1 // Multiply both sides by (y + 5)
xy + 5x = 1 // Distribute x
xy = 1 – 5x // Subtract 5x from both sides
y = (1 – 5x) / x // Divide both sides by x
y = 1/x – 5 // Simplify
f^(-1)(x) = 1/x – 5
Domain: (-∞, 0) ∪ (0, ∞)
Range: (-∞, -5) ∪ (-5, ∞)
Graphical Method:
To find the inverse using a graph:
- Graph the original function f(x) = 1/(x + 5).
- Reflect the graph across the line y = x.
- The resulting graph represents the inverse function f^(-1)(x).
- Observe the graph’s domain and range to determine the inverse’s domain and range.
Note: The graphical method provides a visual representation, but may not provide exact values for domain and range.
Correct Answer:
B) f^(-1)(x) = 1/x – 5; Domain: (-∞, 0) ∪ (0, ∞), Range: (-∞, -5) ∪ (-5, ∞)
Quiz Question:
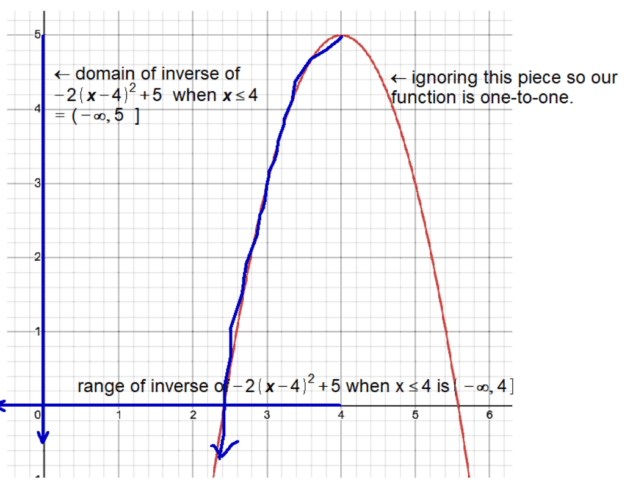
Find the inverse, domain, and range of the function:
f(x) = -2(x-4)² + 5
restricted to x ≤ 4.
Answer Choices:
A) f⁻¹(x) = 4 – √((-x+5)/2); Domain: (-∞, 5], Range: (-∞, 4]
B) f⁻¹(x) = 4 + √((-x+5)/2); Domain: [5, ∞), Range: [4, ∞)
C) f⁻¹(x) = 4 + √((x+5)/2); Domain: (-∞, 5], Range: [4, ∞)
Solution:
Original Function:
f(x) = -2(x-4)² + 5, restricted to x ≤ 4
Step 1: Swap x and y
x = -2(y-4)² + 5
Step 2: Solve for y
(y-4)² = (-x+5)/2
y-4 = ±√((-x+5)/2)
y = 4 ± √((-x+5)/2)
Step 3: Choose the correct branch
Since x ≤ 4, choose the negative branch:
y = 4 – √((-x+5)/2)
Inverse Function:
f⁻¹(x) = 4 – √((-x+5)/2)
Domain and Range:
Domain: (-∞, 5]
Range: (-∞, 4]
The domain restriction x ≤ 4 ensures the function is one-to-one, allowing an inverse to exist. The inverse function is then found by swapping x and y and solving for y.
Correct Answer:
A) f⁻¹(x) = 4 – √((-x+5)/2); Domain: (-∞, 5], Range: (-∞, 4]
Date: 2024-10-27
Time: 10:52 AM
Math Question
Problem:
Let f(x) = √(x − 1) and g(x) = (5x − 10) / (x − 2). What is the solution to f(g(x)) = 1?
Options:
- 1. x = 3
- 2. x = 4
- 3. Does not exist
- 4. x = 5
Solution Explanation:
Step 1: Find g(x):
We know f(g(x)) = √(g(x) − 1). We set this equal to 1: √(g(x) − 1) = 1.
Next, we square both sides of the equation to eliminate the square root:
(g(x) − 1) = 1²
This simplifies to g(x) − 1 = 1.
To isolate g(x), we add 1 to both sides of the equation:
g(x) = 2.
Step 2: Solve for x:
We now set the expression for g(x), which is (5x − 10) / (x − 2), equal to 2:
(5x − 10) / (x − 2) = 2.
To eliminate the denominator, multiply both sides of the equation by (x − 2):
5x − 10 = 2 * (x − 2).
Expand the right side by multiplying 2 with each term inside the parentheses:
5x − 10 = 2x − 4.
Next, subtract 2x from both sides of the equation to collect all x terms on one side:
5x − 2x − 10 = −4
This simplifies to 3x − 10 = −4.
Now, add 10 to both sides to isolate the term with x:
3x = 6.
Finally, divide both sides by 3 to solve for x:
x = 2.
Step 3: Check the solution:
Substituting x = 2 back into g(x) = (5x − 10) / (x − 2), we notice that the denominator becomes zero, which makes g(x) impossible to define at that point.
As a result, the solution does not exist.
We can solve x/(x-1)>0 graphically by looking at where the graph is above the x-axis and writing down the appropriate x-intervals.
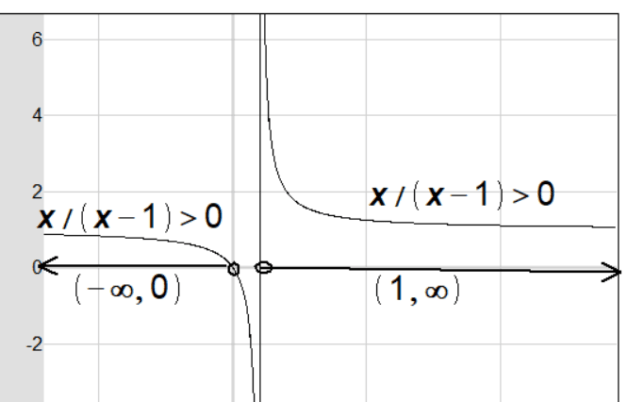
🕒 Answer Date and Time: 2024-11-01 9:00 AM
The correct answer is B) f(g(x)) is decreasing.
Detailed Explanation:
To understand why, let’s break down the given functions and the composite function step by step:
- f(x) = 2x: This is a linear function with a positive slope. It increases as x increases, so over the interval (0, 2), f(x) is increasing.
- g(x) = 1 − x: This is also a linear function but with a negative slope. It decreases as x increases, so over the interval (0, 2), g(x) is decreasing.
Now, we want to find the behavior of the composition f(g(x)). By substituting g(x) into f(x), we get:
f(g(x)) = f(1 − x) = 2(1 − x) = 2 − 2x
This is a linear function with a slope of −2, which is negative. A negative slope indicates that the function is decreasing.
Conclusion: Since f(g(x)) = 2 − 2x has a negative slope, it is decreasing over the interval (0, 2).
So, the composite function f(g(x)) behaves as a decreasing function on (0, 2).
Quiz Question:
A pool fills at a rate given by R(t) = e2t. If the pool’s maximum capacity is 15,000 gallons, what integral should be set up to find the amount of water in the pool at the time that is half of the total time it takes to fill the pool?
Answers:
- A) ∫0ln(30,001) / 2 e2t dt
- B) ∫0ln(15,001) / 4 e2t dt
- C) ∫0ln(30,001) / 4 e2t dt (Correct)
Step-by-step Solution:
Step 1: Set Up the Problem
We are given the rate of change of water filling the pool as R(t) = e2t gallons per unit time. The total capacity of the pool is 15,000 gallons. We need to find the amount of water in the pool at the time that is half of the total time it takes to fill the pool to 15,000 gallons.
Step 2: Find the Total Time T to Fill the Pool
To find the total time T, we need to solve the equation:
∫0T e2t dt = 15,000.
Step 3: Evaluate the Integral
The integral ∫ e2t dt can be solved by direct integration:
∫ e2t dt = (e2t / 2) + C.
Substitute this result into our equation:
[e2T / 2] – [e0 / 2] = 15,000.Simplify:
(e2T – 1) / 2 = 15,000.
Multiply both sides by 2:
e2T – 1 = 30,000.
Add 1 to both sides:
e2T = 30,001.
Step 4: Solve for T
Take the natural logarithm (ln) of both sides:
2T = ln(30,001).
Divide by 2:
T = (ln 30,001) / 2.
Step 5: Find Half of the Time T
We need the time t such that t = T / 2:
t = (ln 30,001) / 4.
Step 6: Set Up the Integral for Half the Time
To find the amount of water at time t, set up the integral:
∫0(ln 30,001) / 4 e2t dt.
Step 7: Evaluate the Integral for Half the Time
We already know how to integrate e2t:
∫ e2t dt = (e2t / 2).
Substitute the limits of integration:
[e(2(ln 30,001) / 4) / 2] – [e0 / 2].Step 8: Simplify the Expression
Simplify e(2(ln 30,001) / 4):
e(ln 30,001 / 2) = √30,001.
Substitute this back into the expression:
(√30,001 / 2) – (1 / 2).
Combine terms:
(√30,001 – 1) / 2.
Final Answer:
The amount of water in the pool at the time t = T / 2 is:
(√30,001 – 1) / 2 gallons.