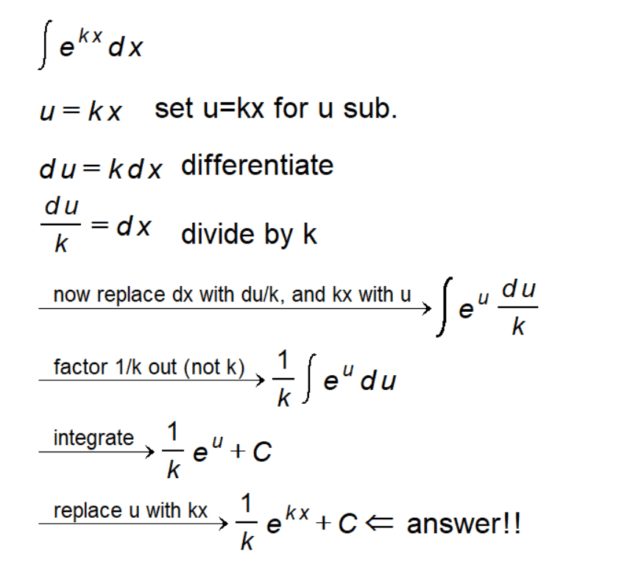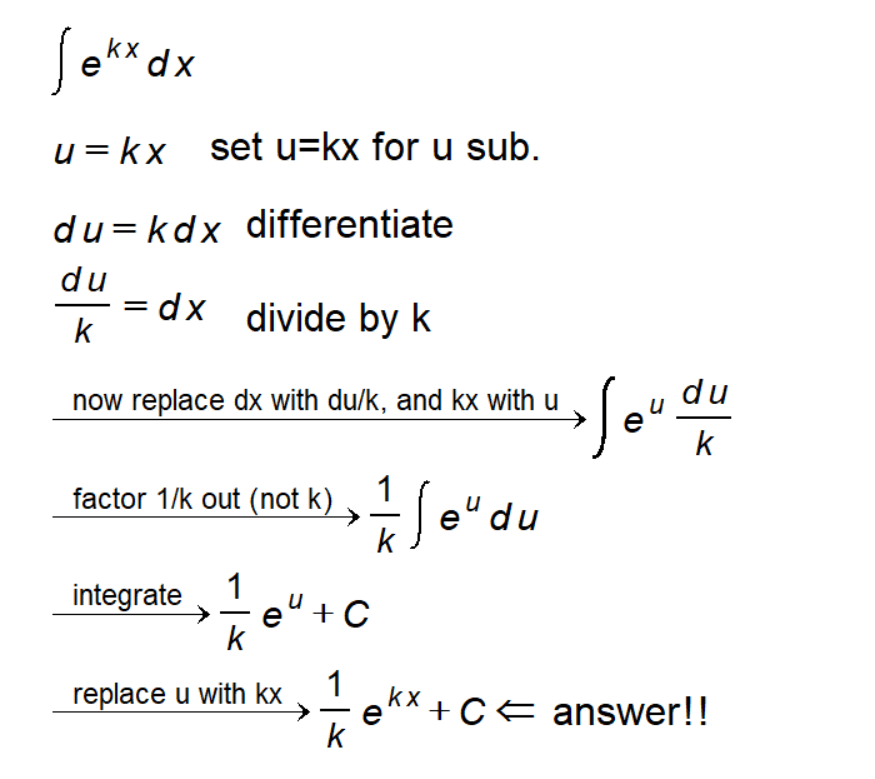Mastering U-Substitution: Integrating ∫ eᵏˣ dx

Unlock the power of u-substitution to effortlessly solve integrals. In this walkthrough, we will explore the step-by-step process to integrate the exponential function eᵏˣ with respect to x utilizing u-substitution, a cornerstone technique in calculus. This method simplifies the integral, making it easier to solve, and is a testament to the beauty and utility of mathematical substitution.

1. Identify the substitution: The first step in u-substitution is identifying the substitution variable. For our integral, we choose u = kx.
2. Differentiate to solve for dx: Differentiate u with respect to x to obtain du = k dx. Now, isolate dx by dividing both sides by k, yielding du/k = dx.
3. Substitute back into the integral: With the expression for dx, substitute back into the original integral: ∫ eᵏˣ dx = ∫ eᵘ du/k.
4. Factor out the constant 1/k: Factor out the constant term 1/k from the integral, resulting in 1/k ∫ eᵘ du.
5. Integrate with respect to u: Now, integrate the expression with respect to u to obtain 1/k eᵘ + C.
6. Substitute the original expression for u: Finally, replace u with the original expression kx, yielding the final solution 1/k eᵏˣ + C.

Through u-substitution, we have elegantly solved the integral of eᵏˣ. This process showcases the transformative power of u-substitution, enabling us to tackle integrals that might initially seem daunting.

The Fundamental Principle: Integrating a Derivative

One of the foundational ideas in calculus is the relationship between differentiation and integration. This relationship is elegantly captured by the equation: ∫ f'(x) dx = f(x). This equation tells us that the integral of the derivative of a function f with respect to x yields the original function f(x) (up to a constant of integration). This principle forms the backbone of many calculus concepts and techniques, including the Fundamental Theorem of Calculus.

As illustrated in the process of u-substitution earlier, understanding the interplay between differentiation and integration allows us to transform complex integrals into simpler, more manageable forms. By recognizing the derivative within the integral, we can often find a straightforward path to evaluating the integral and uncovering the function from which it originated.

Whether you are delving into the areas under curves, analyzing rates of change, or exploring the myriad applications of calculus in science and engineering, this basic principle serves as a guiding light. It encapsulates the essence of calculus, illustrating the harmony between change and accumulation, between the instantaneous and the continuous.