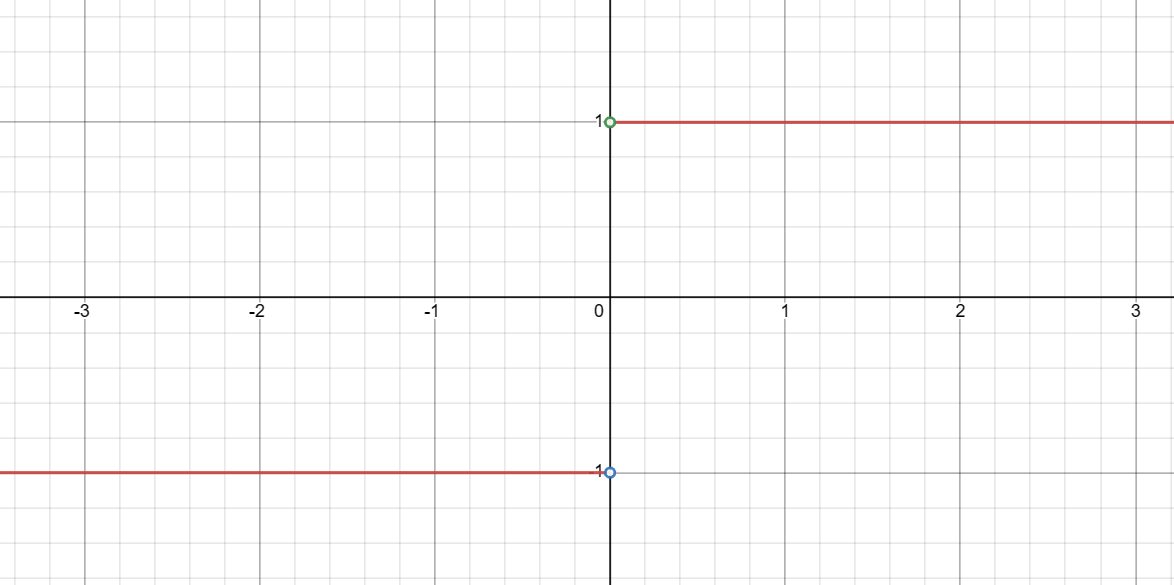Understanding the Limit of |x|/x as x Approaches 0: A Comprehensive Guide
Does the limit of |x|/x exist as x goes to 0?
In symbols: Does lim(x → 0) |x|/x exist?
Since we have absolute value bars, we consider two cases:
- For x < 0:
This means that we drop the bars and write:
lim(x → 0) -x/x = lim(x → 0) -1 = -1
Remember this works because if x = -2, to take the absolute value we write -(-2) = 2 and so on.
Understanding the Limit of the Absolute Value of x Divided by x as x Nears Zero: Case for x > 0
For x > 0:
In this case, the absolute value bars are redundant as x is already positive.
lim(x → 0) x/x = lim(x → 0) 1 = 1
Final Result: Does the Limit of |x|/x as x Approaches 0 Exist?
The limit does not exist. Here’s why:
- For x > 0, the limit is 1.
- For x < 0, the limit is -1.
- At x = 0, the expression |x|/x is undefined because we cannot divide by zero.
Since the limits for x > 0 and x < 0 are different, and the expression is undefined at x = 0, the overall limit as x approaches 0 does not exist.
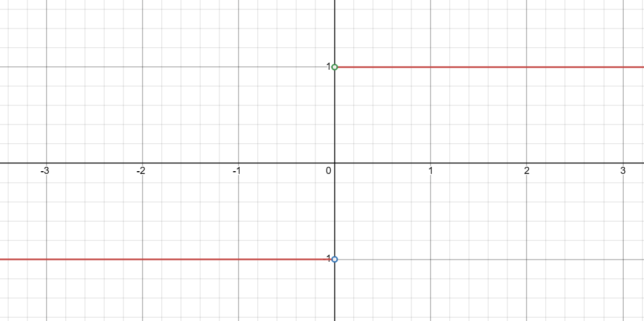
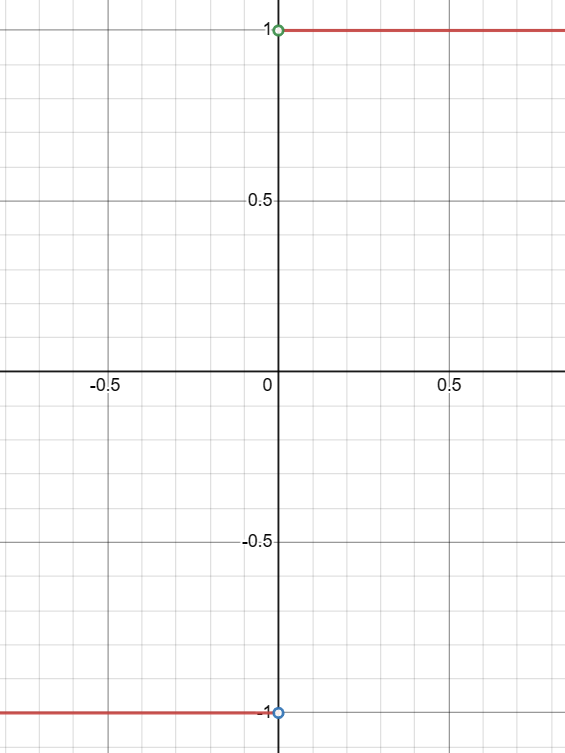
Final Result: Does the Limit of |x|/x as x Approaches 0 Exist?
The limit does not exist. Here’s the complete explanation:
- For x > 0, the limit approaches 1.
- For x < 0, the limit approaches -1.
- The graph has two separate pieces, one for x > 0 and another for x < 0.
- There are “holes” in the graph at the points (0, 1) and (0, -1), indicating the function is undefined at x = 0.
Because of these differing behaviors as x approaches 0 from different sides and the undefined points, the overall limit does not exist.
Domain of the Function |x|/x
- Interval Notation: (-∞, 0) ∪ (0, ∞)
- Set-Builder Notation: { x ∈ R : x ≠ 0 }
- In Words: All real numbers except x = 0