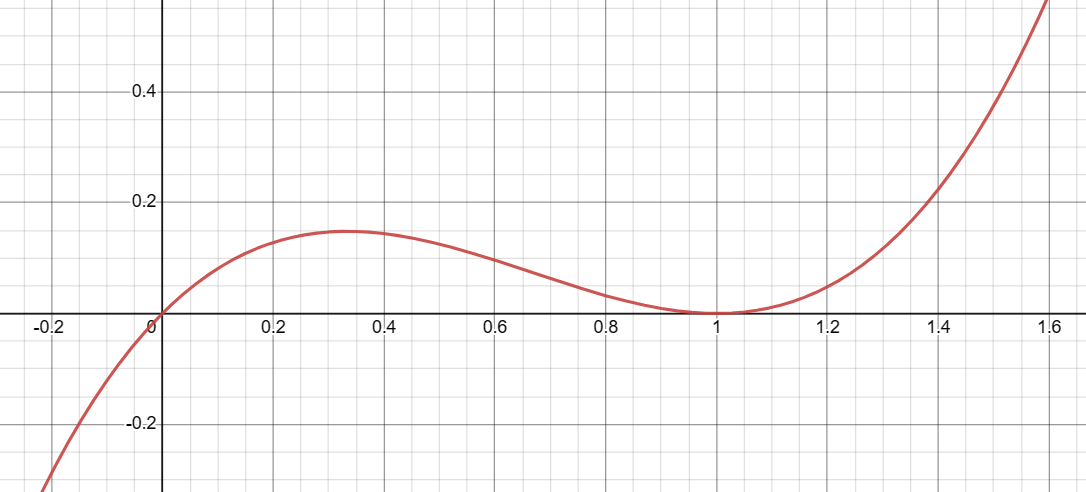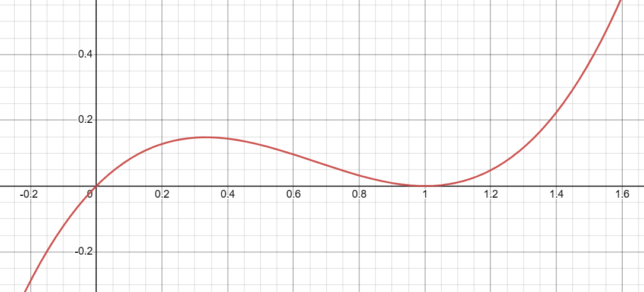
Detailed Analysis of f(x) = x(x-1)² Near x=0
Breaking Down the Factors
The function f(x) = x(x-1)² can be broken down into its individual factors:
- x: This is a simple linear term with a root at x = 0.
- (x-1)²: This is a quadratic term with a double root at x = 1.
Behavior of Individual Factors
- The factor x crosses the x-axis at x = 0 and behaves linearly around this point.
- The factor (x-1)² has a double root at x = 1 and “bounces” off the x-axis at this point. However, around x = 0, it behaves like a regular quadratic function and takes on positive values.
Overall Behavior Near x=0
When x is close to 0, the term x is close to 0 while (x-1)² is close to 1. Therefore, the overall function f(x) = x(x-1)² will be close to 0.
As x approaches 0 from the left or the right, the function approaches 0 from above, because the term (x-1)² is always positive.
Table of Calculations Close to x=0 for f(x) = x(x-1)²
| x Value Near 0 | Value of (x-1)² | Value of f(x) = x(x-1)² |
|---|---|---|
| -0.1 | 1.21 | -0.121 |
| -0.01 | 1.0001 | -0.000010001 |
| -0.001 | 1.000001 | -0.000000001001 |
| 0 | 1 | 0 |
| 0.001 | 1.000001 | 0.000000001001 |
| 0.01 | 1.0001 | 0.000010001 |
| 0.1 | 1.21 | 0.121 |
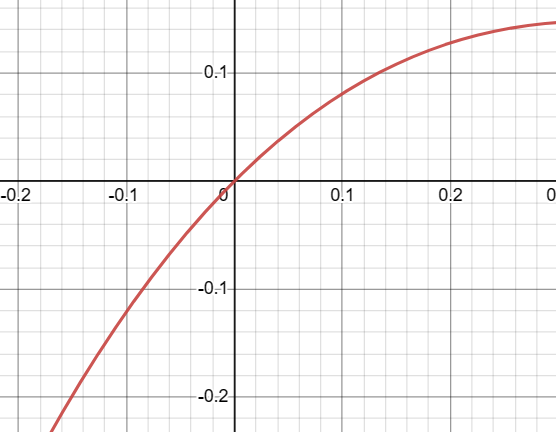
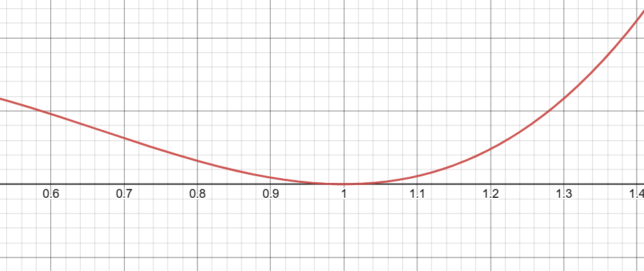
Analysis of f(x) = x(x-1)² Near x=1
Behavior of Individual Factors Near x=1
- The factor x is a linear term that takes the value 1 when x = 1.
- The factor (x-1)² is a quadratic term with a double root at x = 1. It “bounces” off the x-axis at this point.
Overall Behavior Near x=1
When x is close to 1, the term x is close to 1, and (x-1)² is close to 0. Therefore, the overall function f(x) = x(x-1)² will be close to 0.
As x approaches 1 from the left or the right, the function approaches 0 from above, because the term (x-1)² is always non-negative.
Table of Calculations Close to x=1 for f(x) = x(x-1)²
| x Value Near 1 | Value of (x-1)² | Value of f(x) = x(x-1)² |
|---|---|---|
| 0.9 | 0.01 | 0.009 |
| 0.99 | 0.0001 | 0.000099 |
| 0.999 | 0.000001 | 0.000000999 |
| 1 | 0 | 0 |
| 1.001 | 0.000001 | 0.000001001 |
| 1.01 | 0.0001 | 0.000101 |
| 1.1 | 0.01 | 0.011 |
Understanding the Role of Multiplicities in f(x) = x(x-1)²
Exploring Multiplicities
- The factor x has a single root at x = 0 with a multiplicity of 1. This means the function crosses the x-axis linearly at this point.
- The factor (x-1)² has a double root at x = 1 with a multiplicity of 2. This means the function “bounces” off the x-axis at this point, rather than crossing it.
Impact on Overall Behavior
When x is close to 1, both x and (x-1)² are close to 1 and 0, respectively. The multiplicity of 2 for the root at x = 1 causes the function to bounce at this point, rather than crossing the x-axis. This bouncing behavior is a direct result of the multiplicity of the root.
Similarly, the function crosses the x-axis at x = 0 because the root at this point has a multiplicity of 1, which is indicative of a simple, linear crossing.
Thus, the multiplicities of the roots have a significant impact on how the function behaves near those roots.