🔥 Master the Intricacies of Chain Rule: Unveil the Derivative of |x| through √(x²) 📚
Step 1: Understand the Function
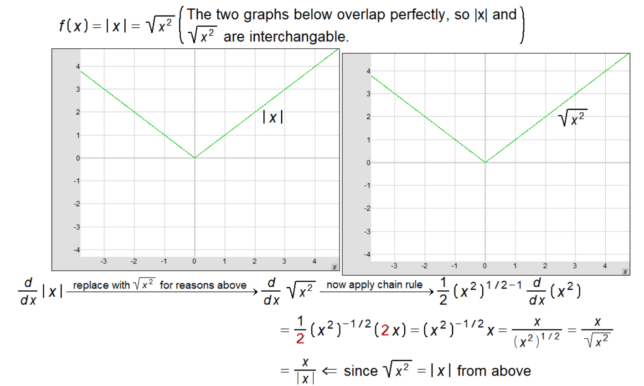
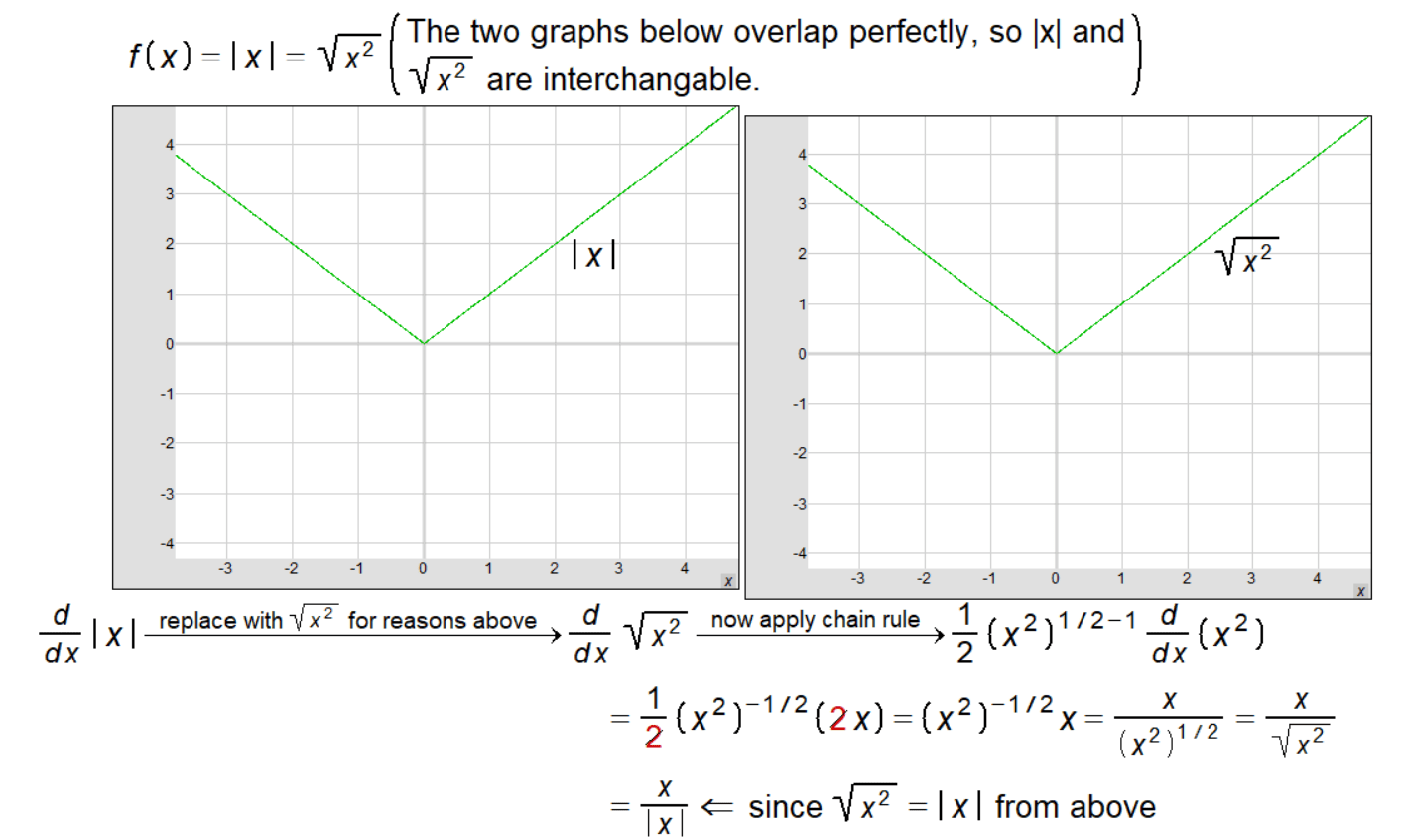
We start with the function f(x) = √(x²), which is an alternate expression for |x|.
Step 2: Decompose the Function
We can think of f(x) as a composite function g(u) where g(u) = √u and u(x) = x².
Step 3: Derivatives of Inner and Outer Functions
We find the derivatives of the inner and outer functions:
- g'(u) = 1 / (2√u)
- u'(x) = 2x
Step 4: Apply the Chain Rule
By Chain Rule, f'(x) = g'(u) × u'(x)
f'(x) = (1 / (2√x²)) × 2x = x / √(x²) = sgn(x)
Step 5: Finalize the Derivative
The derivative f'(x) is 1 for x > 0, -1 for x < 0, and undefined for x = 0.