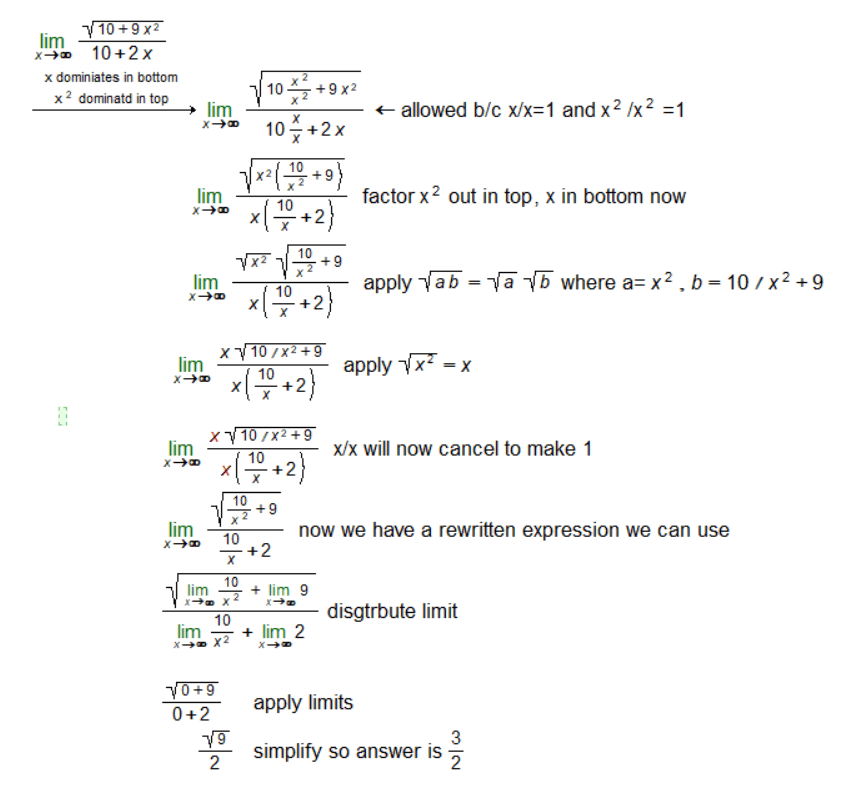Unlock the Secrets of Limits: Part 1
Step 1: Start with the Original Expression
We begin with the original expression \[ \lim_{{x \to \infty}} \frac{\sqrt{10 + 9x^2}}{10 + 2x} \]. This is our starting point.
Step 2: Multiply by \( \frac{x}{x} \) and \( \frac{x^2}{x^2} \)
We multiply the terms in the expression by \( \frac{x}{x} \) and \( \frac{x^2}{x^2} \) because \( \frac{x}{x} = 1 \) and \( \frac{x^2}{x^2} = 1 \).
Step 3: Rewrite the Expression
The expression becomes \[ \lim_{{x \to \infty}} \frac{\sqrt{10 \frac{x^2}{x^2} + 9x^2}}{10 \frac{x}{x} + 2x} \].
Step 4: Factor Out \( x^2 \) in the Numerator and \( x \) in the Denominator
We factor out \( x^2 \) from the terms inside the square root in the numerator and \( x \) from the terms in the denominator. The expression becomes \[ \lim_{{x \to \infty}} \frac{\sqrt{x^2 \left( \frac{10}{x^2} + 9 \right)}}{x \left( \frac{10}{x} + 2 \right)} \].
Step 5: Apply the Square Root Property \( \sqrt{ab} = \sqrt{a} \sqrt{b} \)
We apply the square root property to get \[ \lim_{{x \to \infty}} \frac{\sqrt{x^2} \sqrt{\frac{10}{x^2} + 9}}{x \left( \frac{10}{x} + 2 \right)} \].
Step 6: Simplify \( \sqrt{x^2} \) to \( x \)
We simplify \( \sqrt{x^2} \) to \( x \), resulting in \[ \lim_{{x \to \infty}} \frac{x \sqrt{\frac{10}{x^2} + 9}}{x \left( \frac{10}{x} + 2 \right)} \].
Step 7: Cancel \( x \) from the Numerator and Denominator
We cancel \( x \) from the numerator and the denominator, which is allowed because \( \frac{x}{x} = 1 \).
Unlock the Secrets of Limits: Part 2
Step 8: Rewrite the Expression After Canceling \( x \)
The expression becomes \[ \lim_{{x \to \infty}} \frac{\sqrt{\frac{10}{x^2} + 9}}{\frac{10}{x} + 2} \].
Step 9: Distribute the Limit to Each Term
We distribute the limit to each term in the numerator and the denominator.
Step 10: Evaluate \( \lim_{{x \to \infty}} \frac{10}{x^2} \)
The limit of \( \frac{10}{x^2} \) as \( x \) approaches infinity is 0.
Step 11: Evaluate \( \lim_{{x \to \infty}} \frac{10}{x} \)
The limit of \( \frac{10}{x} \) as \( x \) approaches infinity is 0.
Step 12: Evaluate \( \lim_{{x \to \infty}} 9 \) and \( \lim_{{x \to \infty}} 2 \)
The limits of 9 and 2 as \( x \) approaches infinity are 9 and 2, respectively.
Step 13: Substitute the Limits into the Expression
The expression becomes \( \frac{\sqrt{0 + 9}}{0 + 2} \).
Step 14: Simplify the Expression
The expression simplifies to \( \frac{\sqrt{9}}{2} \).
Step 15: Conclude
After these detailed steps, we find that the limit of \( \frac{\sqrt{10 + 9x^2}}{10 + 2x} \) as \( x \) approaches infinity is \( \frac{3}{2} \).
Unlock the Secrets of Limits: Part 1
Step 1: Start with the Original Expression
We begin with the original expression \[ \lim_{{x \to \infty}} \frac{\sqrt{5 + 4x^2}}{5 + x} \]. This is our starting point.
Step 2: Multiply by \( \frac{x}{x} \) and \( \frac{x^2}{x^2} \)
We multiply the terms in the expression by \( \frac{x}{x} \) and \( \frac{x^2}{x^2} \) because \( \frac{x}{x} = 1 \) and \( \frac{x^2}{x^2} = 1 \).
Step 3: Rewrite the Expression
The expression becomes \[ \lim_{{x \to \infty}} \frac{\sqrt{5 \frac{x^2}{x^2} + 4x^2}}{5 \frac{x}{x} + x} \].
Step 4: Factor Out \( x^2 \) in the Numerator and \( x \) in the Denominator
We factor out \( x^2 \) from the terms inside the square root in the numerator and \( x \) from the terms in the denominator. The expression becomes \[ \lim_{{x \to \infty}} \frac{\sqrt{x^2 \left( \frac{5}{x^2} + 4 \right)}}{x \left( \frac{5}{x} + 1 \right)} \].
Step 5: Apply the Square Root Property \( \sqrt{ab} = \sqrt{a} \sqrt{b} \)
We apply the square root property to get \[ \lim_{{x \to \infty}} \frac{\sqrt{x^2} \sqrt{\frac{5}{x^2} + 4}}{x \left( \frac{5}{x} + 1 \right)} \].
Step 6: Simplify \( \sqrt{x^2} \) to \( x \)
We simplify \( \sqrt{x^2} \) to \( x \), resulting in \[ \lim_{{x \to \infty}} \frac{x \sqrt{\frac{5}{x^2} + 4}}{x \left( \frac{5}{x} + 1 \right)} \].
Step 7: Cancel \( x \) from the Numerator and Denominator
We cancel \( x \) from the numerator and the denominator, which is allowed because \( \frac{x}{x} = 1 \).
Unlock the Secrets of Limits: Part 2
Step 8: Rewrite the Expression After Canceling \( x \)
The expression becomes \[ \lim_{{x \to \infty}} \frac{\sqrt{\frac{5}{x^2} + 4}}{\frac{5}{x} + 1} \].
Step 9: Distribute the Limit to Each Term
We distribute the limit to each term in the numerator and the denominator.
Step 10: Evaluate \( \lim_{{x \to \infty}} \frac{5}{x^2} \)
The limit of \( \frac{5}{x^2} \) as \( x \) approaches infinity is 0.
Step 11: Evaluate \( \lim_{{x \to \infty}} \frac{5}{x} \)
The limit of \( \frac{5}{x} \) as \( x \) approaches infinity is 0.
Step 12: Evaluate \( \lim_{{x \to \infty}} 4 \) and \( \lim_{{x \to \infty}} 1 \)
The limits of 4 and 1 as \( x \) approaches infinity are 4 and 1, respectively.
Step 13: Substitute the Limits into the Expression
The expression becomes \( \frac{\sqrt{0 + 4}}{0 + 1} \).
Step 14: Simplify the Expression
The expression simplifies to \( \frac{\sqrt{4}}{1} \).
Step 15: Conclude
After these detailed steps, we find that the limit of \( \frac{\sqrt{5 + 4x^2}}{5 + x} \) as \( x \) approaches infinity is \( \frac{2}{1} = 2 \).