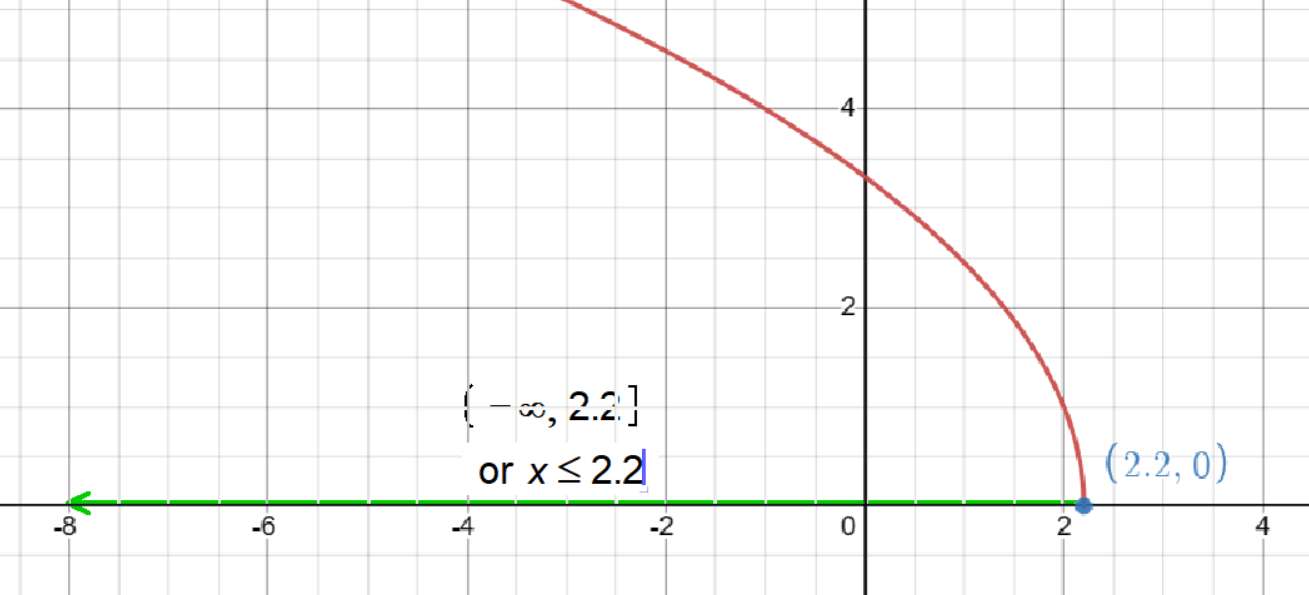Finding the Domain of √(-5x + 11)
Here are the detailed steps to find the domain of the function √(-5x + 11).
Step 1: Identify the Expression Under the Square Root
The expression under the square root is -5x + 11.
Step 2: Set the Expression to be Non-Negative
For the square root to be real, the expression under it must be non-negative. This leads to the inequality -5x + 11 ≥ 0.
Step 3: Isolate x
To find the values of x that satisfy this inequality, we isolate x on one side.
- First, move all terms involving x to one side and constants to the other: -5x ≥ -11.
- Next, divide both sides by -5, remembering to flip the inequality sign: x ≤ 11/5.
- Finally, simplify the fraction: x ≤ 2.2.
Conclusion
The domain of the function √(-5x + 11) is x ≤ 2.2.
Converting Inequality to Interval Notation: Symbol by Symbol
This section explains how to convert the inequality x ≤ 2.2 into interval notation, focusing on each symbol.
Step 1: Understand the ‘≤’ Symbol
The symbol ‘≤’ is a combination of ‘<' (less than) and '=' (equal to). It means 'less than or equal to'.
Step 2: Break Down the Symbol
We can break down ‘≤’ into two parts: ‘less than’ represented by ‘<' and 'equal to' represented by '='.
Step 3: Convert ‘<' to Interval Notation
In interval notation, ‘less than’ is represented by using a round parenthesis ‘)’. If the inequality was x < 2.2, the interval would be (-∞, 2.2).
Step 4: Convert ‘=’ to Interval Notation
In interval notation, ‘equal to’ is represented by using a square bracket ‘]’. If the inequality was x = 2.2, the interval would be [2.2, 2.2].
Step 5: Combine Both Symbols
Since the original inequality is ‘less than or equal to’, we combine both symbols in interval notation. The interval becomes (-∞, 2.2] which includes both ‘less than’ and ‘equal to’.
Conclusion
The inequality x ≤ 2.2 is represented in interval notation as (-∞, 2.2].
Converting Inequality to Set-Builder Notation: Symbol by Symbol
This section explains how to convert the inequality x ≤ 2.2 into set-builder notation, focusing on each symbol.
Step 1: Understand the ‘≤’ Symbol
The symbol ‘≤’ is a combination of ‘<' (less than) and '=' (equal to). It means 'less than or equal to'.
Step 2: Break Down the Symbol
We can break down ‘≤’ into two parts: ‘less than’ represented by ‘<' and 'equal to' represented by '='.
Step 3: Convert ‘<' to Set-Builder Notation
In set-builder notation, ‘less than’ would be expressed as {x | x < 2.2}.
Step 4: Convert ‘=’ to Set-Builder Notation
In set-builder notation, ‘equal to’ would be expressed as {x | x = 2.2}.
Step 5: Combine Both Symbols
Since the original inequality is ‘less than or equal to’, we combine both symbols in set-builder notation. The set becomes {x | x ≤ 2.2}.
Conclusion
The inequality x ≤ 2.2 is represented in set-builder notation as {x | x ≤ 2.2}.
Unlocking the Calculus Behind \( \sqrt{-5x + 11} \): A Step-by-Step Guide to Finding Its Derivative
Step 1: Rewrite the Function in Exponential Form
We start by rewriting \( \sqrt{-5x + 11} \) in exponential form to make it easier to differentiate. The square root of a number is the same as raising that number to the power of \( \frac{1}{2} \).
\[ \sqrt{-5x + 11} = (-5x + 11)^{\frac{1}{2}} \]
Step 2: Understand the Chain Rule
The chain rule is a fundamental principle in calculus used for differentiating composite functions. It states that the derivative of \( f(g(x)) \) is \( f'(g(x)) \times g'(x) \).
\[ (f(g(x)))’ = f'(g(x)) \times g'(x) \]
Step 3: Identify the Outer and Inner Functions
In our function \( (-5x + 11)^{\frac{1}{2}} \), the outer function is \( f(u) = u^{\frac{1}{2}} \) and the inner function is \( g(x) = -5x + 11 \).
Step 4: Differentiate the Outer Function
We first find the derivative of the outer function \( f(u) = u^{\frac{1}{2}} \) with respect to \( u \).
\[ f'(u) = \frac{1}{2} u^{-\frac{1}{2}} \]
Step 5: Differentiate the Inner Function
Next, we find the derivative of the inner function \( g(x) = -5x + 11 \) with respect to \( x \).
\[ g'(x) = -5 \]
Step 6: Apply the Chain Rule
Now we apply the chain rule by multiplying the derivative of the outer function evaluated at the inner function by the derivative of the inner function.
\[ \frac{d}{dx} \left( (-5x + 11)^{\frac{1}{2}} \right) = \frac{1}{2} (-5x + 11)^{-\frac{1}{2}} \times (-5) \]
Step 7: Simplify the Expression
Finally, we simplify the expression to get the derivative of the original function.
\[ \frac{-5}{2} (-5x + 11)^{-\frac{1}{2}} = -\frac{5}{2\sqrt{-5x + 11}} \]
Conclusion
The derivative of \( \sqrt{-5x + 11} \) is \( -\frac{5}{2\sqrt{-5x + 11}} \).
Why the Derivative of \( \sqrt{-5x + 11} \) Is Not Defined at \( x = 2.2 \): A Detailed Explanation
Step 1: Recall the Original Function
The original function is \( \sqrt{-5x + 11} \), which we rewrote as \( (-5x + 11)^{\frac{1}{2}} \) for differentiation.
Step 2: Examine the Derivative
The derivative we found is \( -\frac{5}{2\sqrt{-5x + 11}} \).
Step 3: Identify the Denominator
The derivative has a denominator of \( 2\sqrt{-5x + 11} \). For the derivative to be defined, this denominator cannot be zero.
Step 4: Set the Denominator Equal to Zero
Setting \( 2\sqrt{-5x + 11} = 0 \) and solving, we find that the denominator is zero when \( x = 2.2 \).
Step 5: Understand the Implication
Because the denominator of the derivative is zero at \( x = 2.2 \), the derivative is undefined at this point.
Conclusion
The derivative of \( \sqrt{-5x + 11} \) is not defined at \( x = 2.2 \) because the denominator of the derivative becomes zero, making the expression undefined.