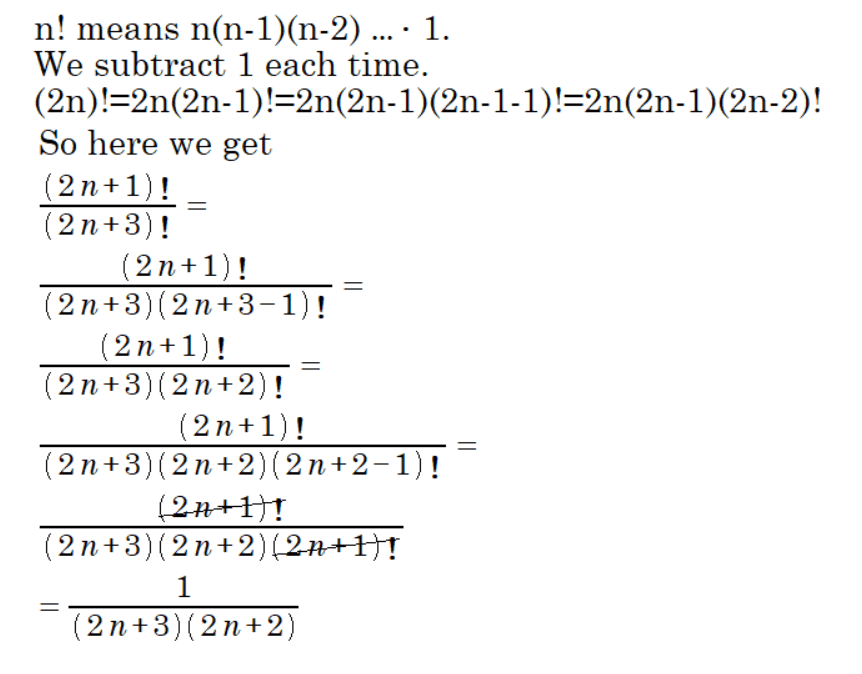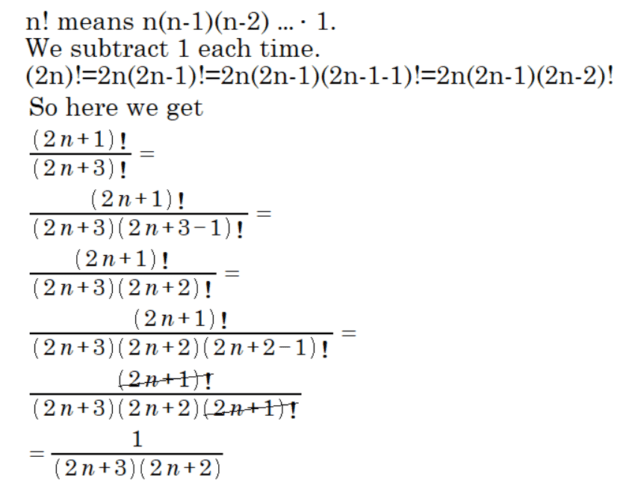
<div>
Understanding the simplification of factorials is crucial for students and professionals engaged in mathematical fields. The image provided presents a step-by-step process for simplifying the ratio of two factorials: (2n+1)! divided by (2n+3)!. Starting with the definition of a factorial as the product of all positive integers up to a given number, the simplification uses the property that a factorial can be expanded and thus, parts of it can be canceled out when divided by another factorial with a common term. The process is meticulously carried out to reach the simplest form of 1 over (2n+3)(2n+2), which is then further reduced to 1 over 2(2n+3)(n+1). This transformation demonstrates the beauty and elegance of mathematical manipulation and serves as an educational example for those learning to navigate through algebraic expressions involving factorials.
</div>