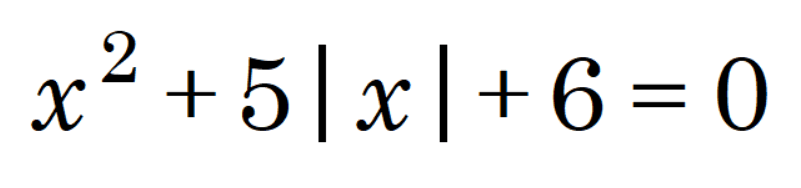Solving Quadratic Equations with Absolute Values
————————————————
This process involves breaking down a quadratic equation with absolute values to find its solutions based on different cases.
Given quadratic expression:
x² + 5|x| + 6 = 0
Case 1: When x is less than zero
——————————–
To solve for x when x is negative, replace x with -x:
x² – 5x + 6 = 0
By factorizing the quadratic expression, you get:
(x – 2)(x – 3) = 0
Thus, the solutions in this case are:
x = 2
x = 3
Case 2: When x is greater than or equal to zero
———————————————–
For non-negative x, you can drop the absolute value bars, resulting in the following quadratic expression:
x² + 5x + 6 = 0
By factorizing this expression, you get:
(x + 3)(x + 2) = 6
This leads to the following solutions:
x = -3
x = -2
Common Solution
—————
In both cases, you derive solutions for the given quadratic equation involving absolute values. This approach highlights the need to consider both positive and negative values of x, using factorization to find the roots of the quadratic expressions.
All of this is correct???? Except the graph of this function shows it has no real roots.
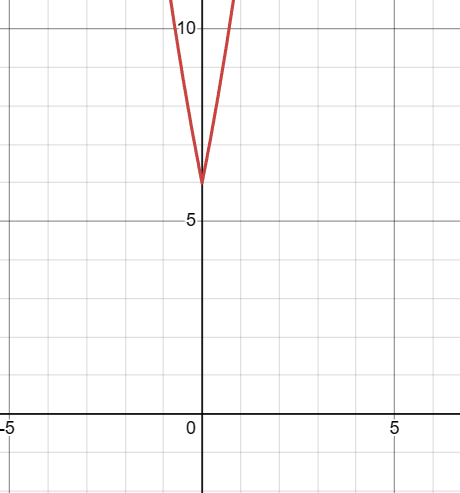
WHen we drop the bars and write -x for x, we extend the parabola in a way that doesn’t match the original:
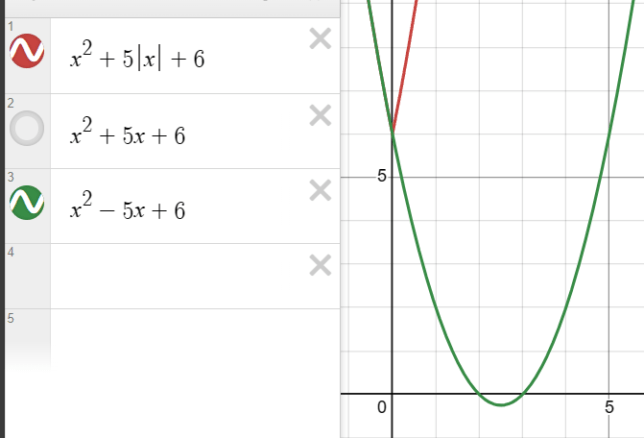
When we drop the bars and write x for |x| for x>=0, we extend the curve in a way that doesn’t match the original:
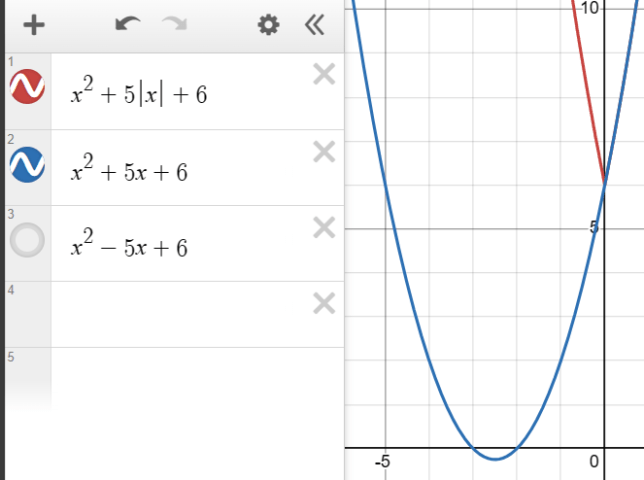
When we drop the bars and write x<0, we have to remember to input negative values for x, as in (-1)^2-5(-1)+6 and then we get a positive value, so it’s all sensible then.