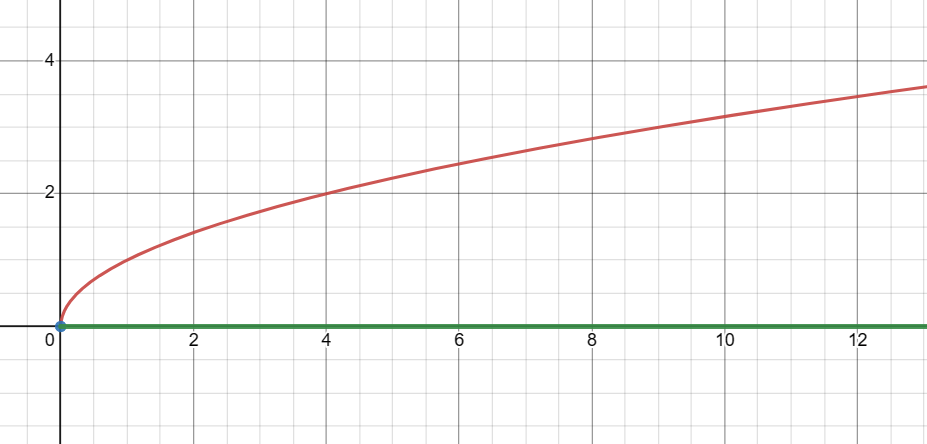
Unlock the Mysteries of the Square Root Graph: √x
Soviet Joke: In Soviet Russia, square root takes you! 🇷🇺
Decoding the Domain: Why x ≥ 0
- Identify the Radicand: In the function √x, the radicand (the number under the square root) is x.
- Set the Radicand ≥ 0: The square root of a negative number is not defined in the real number system, so x must be greater than or equal to zero.
- Domain: The domain of √x is x ≥ 0.
Unlocking the Mysteries: Additional Graph Features
- Range: The range of √x is y ≥ 0. The graph starts at the origin (0,0) and extends infinitely upwards and to the right.
- Quadrants: The graph is located in the 1st quadrant.
- Curve Shape: The graph is a curve that starts at the origin and extends infinitely to the right, getting gradually flatter as x increases.
- End Behavior: As x approaches infinity, y also approaches infinity, but at a decreasing rate.
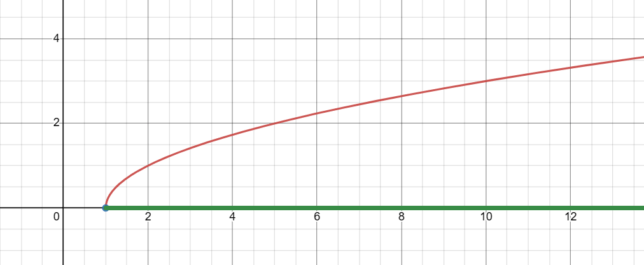
Unlock the Secrets of the Transformed Square Root Graph: √(x-1)
Soviet Joke: In Soviet Russia, square root shifts you! 🇷🇺
Deciphering the Domain: Why x ≥ 1
- Identify the Radicand: In the function √(x-1), the radicand (the number under the square root) is x-1.
- Set the Radicand ≥ 0: The square root of a negative number is not defined in the real number system, so x-1 must be greater than or equal to zero.
- Solve for x: Solving the inequality x-1 ≥ 0 gives x ≥ 1.
- Domain: The domain of √(x-1) is x ≥ 1.
Unlocking the Mysteries: Additional Graph Features
- Range: The range of √(x-1) is y ≥ 0. The graph starts at the point (1,0) and extends infinitely upwards and to the right.
- Quadrants: The graph is located in the 1st quadrant.
- Curve Shape: The graph is a curve that starts at the point (1,0) and extends infinitely to the right, getting gradually flatter as x increases.
- End Behavior: As x approaches infinity, y also approaches infinity, but at a decreasing rate.
- Shift: Compared to the graph of √x, this graph is shifted one unit to the right due to the “-1” in the radicand.
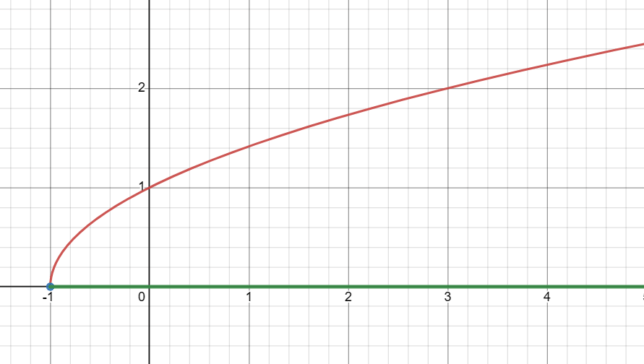
Unlock the Mysteries of the Transformed Square Root Graph: √(x+1)
Soviet Joke: In Soviet Russia, square root shifts you! 🇷🇺
Deciphering the Domain: Why x ≥ -1
- Identify the Radicand: In the function √(x+1), the radicand (the number under the square root) is x+1.
- Set the Radicand ≥ 0: The square root of a negative number is not defined in the real number system, so x+1 must be greater than or equal to zero.
- Solve for x: Solving the inequality x+1 ≥ 0 gives x ≥ -1.
- Domain: The domain of √(x+1) is x ≥ -1.
Unlocking the Mysteries: Additional Graph Features
- Range: The range of √(x+1) is y ≥ 0. The graph starts at the point (-1,0) and extends infinitely upwards and to the right.
- Quadrants: The graph is located in the 1st and 2nd quadrants.
- Curve Shape: The graph is a curve that starts at the point (-1,0) and extends infinitely to the right, getting gradually flatter as x increases.
- End Behavior: As x approaches infinity, y also approaches infinity, but at a decreasing rate.
- Shift: Compared to the graph of √x, this graph is shifted one unit to the left due to the “+1” in the radicand.
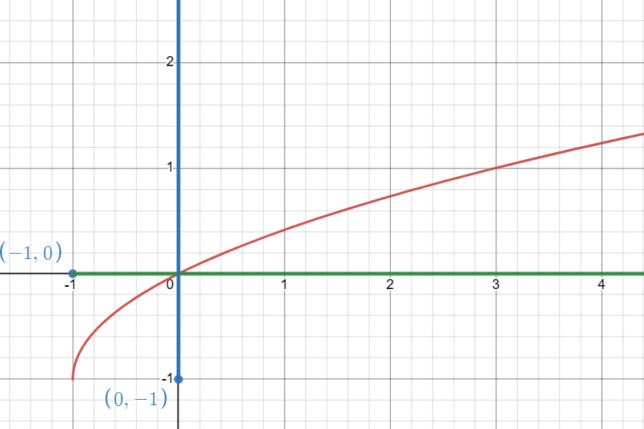
Unveil the Mysteries of the Transformed Square Root Graph: √(x+1) – 1
Soviet Joke: In Soviet Russia, square root shifts you! 🇷🇺
Deciphering the Domain: Why x ≥ -1
- Identify the Radicand: In the function √(x+1) – 1, the radicand (the number under the square root) is x+1.
- Set the Radicand ≥ 0: The square root of a negative number is not defined in the real number system, so x+1 must be greater than or equal to zero.
- Solve for x: Solving the inequality x+1 ≥ 0 gives x ≥ -1.
- Domain: The domain of √(x+1) – 1 is x ≥ -1.
Unlocking the Mysteries: Additional Graph Features
- Range: The range of √(x+1) – 1 is y ≥ -1. The graph starts at the point (-1,-1) and extends infinitely upwards and to the right.
- Curve Shape: The graph is a curve that starts at the point (-1,-1) and extends infinitely to the right, getting gradually flatter as x increases.
- End Behavior: As x approaches infinity, y also approaches infinity.
- Shift: Compared to the graph of √x, this graph is shifted one unit to the left and one unit down due to the “+1” in the radicand and the “-1” subtracted from the function.
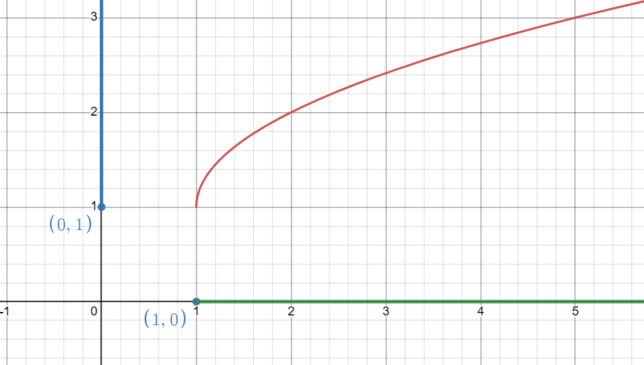
Unveil the Mysteries of the Transformed Square Root Graph: √(x-1) + 1
Soviet Joke: In Soviet Russia, square root shifts you! 🇷🇺
Deciphering the Domain: Why x ≥ 1
- Identify the Radicand: In the function √(x-1) + 1, the radicand (the number under the square root) is x-1.
- Set the Radicand ≥ 0: The square root of a negative number is not defined in the real number system, so x-1 must be greater than or equal to zero.
- Solve for x: Solving the inequality x-1 ≥ 0 gives x ≥ 1.
- Domain: The domain of √(x-1) + 1 is x ≥ 1.
Unlocking the Mysteries: Additional Graph Features
- Range: The range of √(x-1) + 1 is y ≥ 1. The graph starts at the point (1,1) and extends infinitely upwards and to the right.
- Curve Shape: The graph is a curve that starts at the point (1,1) and extends infinitely to the right, getting gradually flatter as x increases.
- End Behavior: As x approaches infinity, y also approaches 1, but at a decreasing rate.
- Shift: Compared to the graph of √x, this graph is shifted one unit to the right and one unit up due to the “+1” added to the function and the “-1” in the radicand.
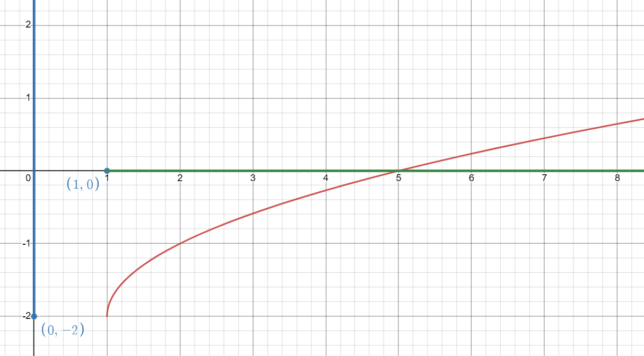
Uncover the Secrets of the Transformed Square Root Graph: √(x-1) – 2
Soviet Joke: In Soviet Russia, square root shifts you! 🇷🇺
Deciphering the Domain: Why x ≥ 1
- Identify the Radicand: In the function √(x-1) – 2, the radicand (the number under the square root) is x-1.
- Set the Radicand ≥ 0: The square root of a negative number is not defined in the real number system, so x-1 must be greater than or equal to zero.
- Solve for x: Solving the inequality x-1 ≥ 0 gives x ≥ 1.
- Domain: The domain of √(x-1) – 2 is x ≥ 1.
Unlocking the Secrets: Additional Graph Features
- Range: The range of √(x-1) – 2 is y ≥ -2. The graph starts at the point (1,-2) and extends infinitely upwards and to the right.
- Curve Shape: The graph is a curve that starts at the point (1,-2) and extends infinitely to the right, getting gradually flatter as x increases.
- End Behavior: As x approaches infinity, y also approaches -2, but at a decreasing rate.
- Shift: Compared to the graph of √x, this graph is shifted one unit to the right and two units down due to the “+2” added to the function and the “-1” in the radicand.