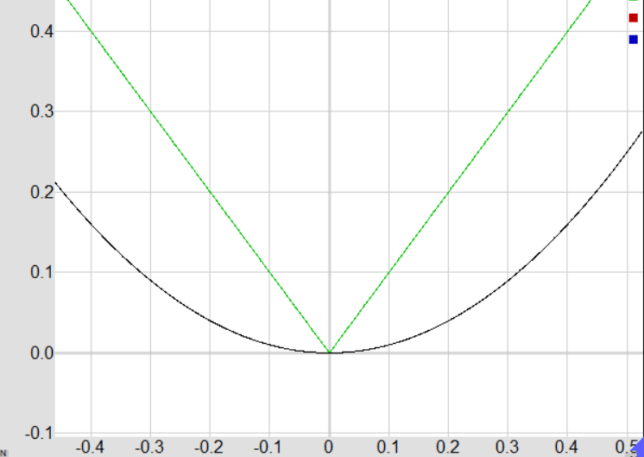
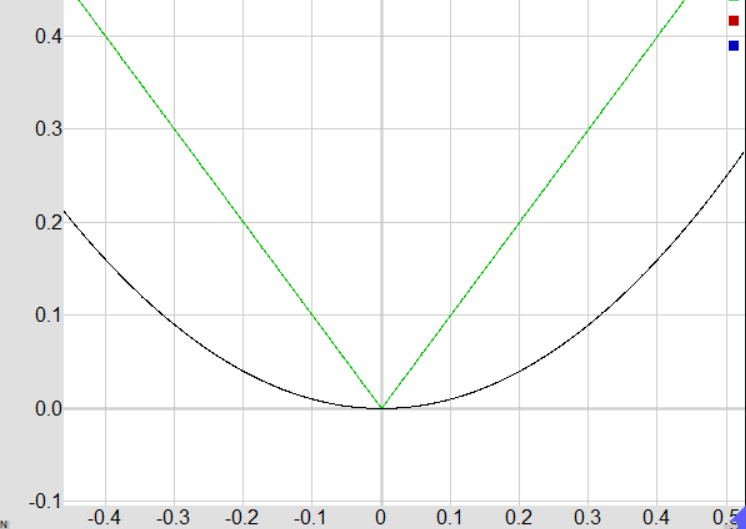
Differentiability of f(x) = x² vs f(x) = |x| at x = 0
f(x) = x²
1. Differentiability: The function f(x) = x² is differentiable at x = 0. Its derivative f'(x) = 2x is well-defined and unique at x = 0, making it f'(0) = 0.
2. Graph: The graph of f(x) = x² is smooth and has a well-defined tangent line at x = 0, which is a horizontal line.
f(x) = |x|
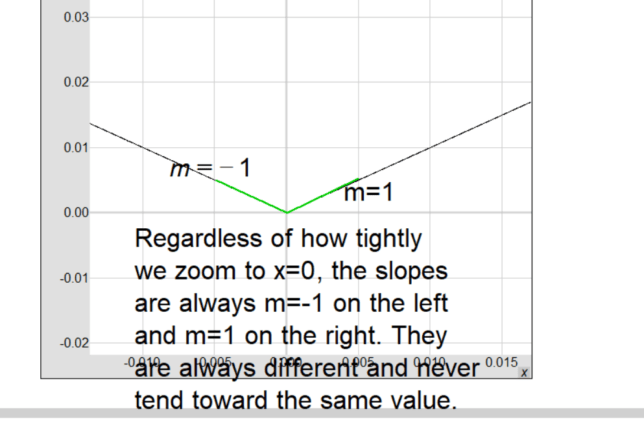
1. Differentiability: The function f(x) = |x| is not differentiable at x = 0. This is because the slope of the function changes abruptly at x = 0, making the derivative undefined.
2. Graph: The graph of f(x) = |x| has a sharp corner at x = 0, indicating that there is no unique tangent line at that point.
Conclusion
The differentiability of a function at a point can be visually confirmed by the smoothness of its graph and the existence of a unique tangent line at that point. The function f(x) = x² meets these criteria at x = 0, while f(x) = |x| does not.
Computing the Slope Around x = 0 for f(x) = |x|
Using x = -0.01
To find the slope between x = 0 and x = -0.01, we use the formula for the average rate of change:
Slope₁ = (f(0) – f(-0.01)) / (0 – (-0.01))
Slope₁ = (0 – |-0.01|) / (0 + 0.01)
Slope₁ = (0 – 0.01) / 0.01
Slope₁ = -0.01 / 0.01
Slope₁ = -1
Using x = 0.01
To find the slope between x = 0 and x = 0.01, we use the same formula:
Slope₂ = (f(0.01) – f(0)) / (0.01 – 0)
Slope₂ = (|0.01| – 0) / 0.01
Slope₂ = 0.01 / 0.01
Slope₂ = 1
Conclusion
The slopes around x = 0 for f(x) = |x| change drastically even when using points very close to x = 0. The slope changes from -1 to 1, indicating that the function is not differentiable at x = 0.
Computing the Slope Around x = 0 for f(x) = x²
Using x = -0.01
To find the slope between x = 0 and x = -0.01, we use the formula for the average rate of change:
Slope₁ = (f(0) – f(-0.01)) / (0 – (-0.01))
Slope₁ = (0 – (-0.01)²) / (0 + 0.01)
Slope₁ = (0 – 0.0001) / 0.01
Slope₁ = -0.0001 / 0.01
Slope₁ = -0.01
Using x = 0.01
To find the slope between x = 0 and x = 0.01, we use the same formula:
Slope₂ = (f(0.01) – f(0)) / (0.01 – 0)
Slope₂ = (0.01² – 0) / 0.01
Slope₂ = 0.0001 / 0.01
Slope₂ = 0.01
Conclusion
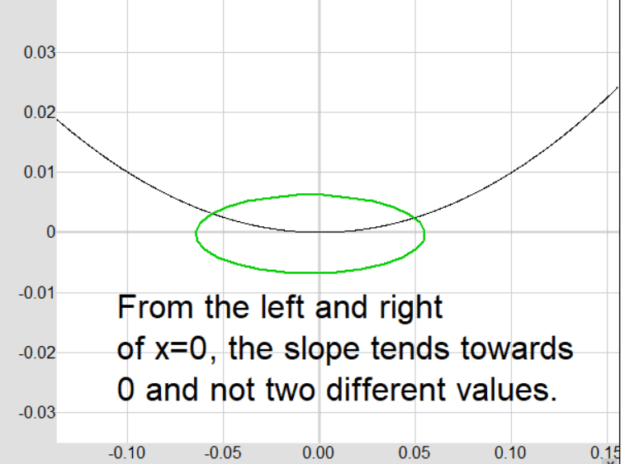
The slopes around x = 0 for f(x) = x² are consistent and do not change drastically when using points very close to x = 0. The slope changes from -0.01 to 0.01, indicating that the function is differentiable at x = 0. This is in contrast to f(x) = |x|, where the slopes changed drastically from -1 to 1.
Computing the Slope Around x = 0 for f(x) = x² Using Closer Points
Using x = -0.001
To find the slope between x = 0 and x = -0.001, we use the formula for the average rate of change:
Slope₁ = (f(0) – f(-0.001)) / (0 – (-0.001))
Slope₁ = (0 – (-0.001)²) / (0 + 0.001)
Slope₁ = (0 – 0.000001) / 0.001
Slope₁ = -0.000001 / 0.001
Slope₁ = -0.001
Using x = 0.001
To find the slope between x = 0 and x = 0.001, we use the same formula:
Slope₂ = (f(0.001) – f(0)) / (0.001 – 0)
Slope₂ = (0.001² – 0) / 0.001
Slope₂ = 0.000001 / 0.001
Slope₂ = 0.001
Conclusion
The slopes around x = 0 for f(x) = x² remain consistent even when using points extremely close to x = 0. The slope changes from -0.001 to 0.001, further confirming that the function is differentiable at x = 0.