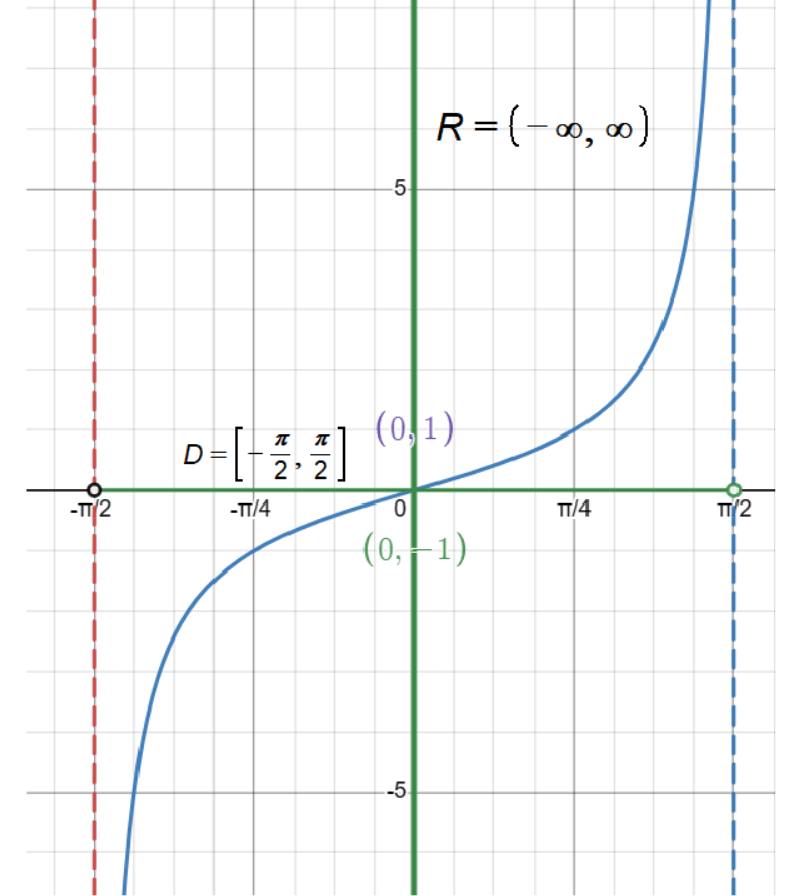
Zooming in on the Middle Branch of tan(x) 🧐
Why the Middle Branch is Special 🌟
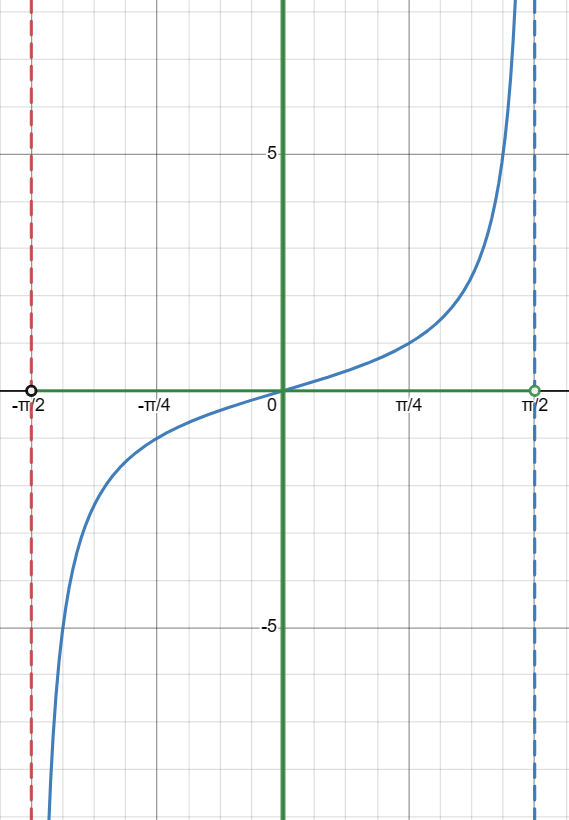
The middle branch of the tan(x) graph is a critical focal point for understanding the behavior of this function. It passes through the origin (0, 0) and serves as the basic building block for the entire graph.
Domain and Range of the Middle Branch 📊
For the middle branch, the domain is all real numbers x in the open interval (-π/2, π/2). The range is all real numbers, extending from -∞ to +∞.
Graph Behavior 📈
The middle branch of the tan(x) graph starts from negative infinity, rises through zero at the origin, and continues to positive infinity. This continuous increase results in a steep incline as you move away from the origin in either direction.
Key Insights 📚
Understanding the behavior of the middle branch of tan(x) helps clarify the overall structure of the function. The middle branch is where the function is defined for x between -π/2 and π/2, avoiding the vertical asymptotes that occur at these boundary points. It provides an essential model that repeats at intervals of π across the entire graph.
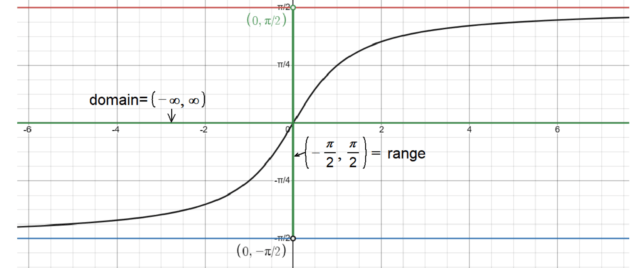
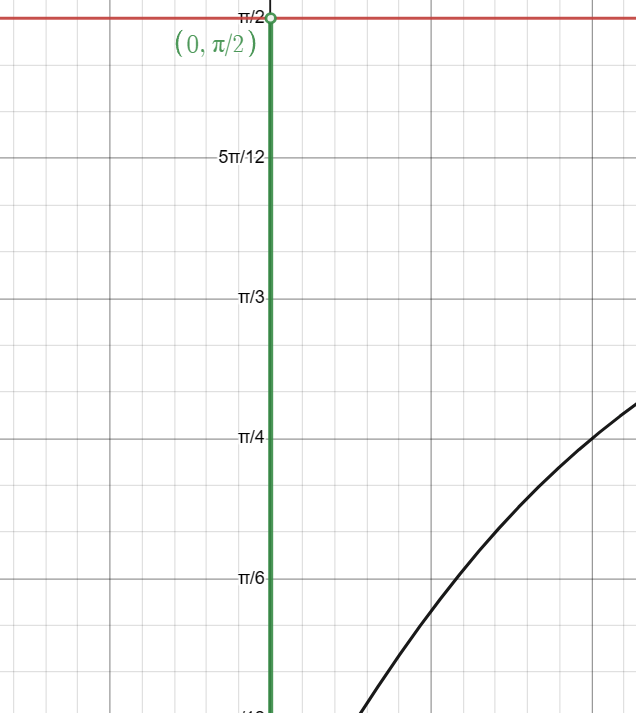
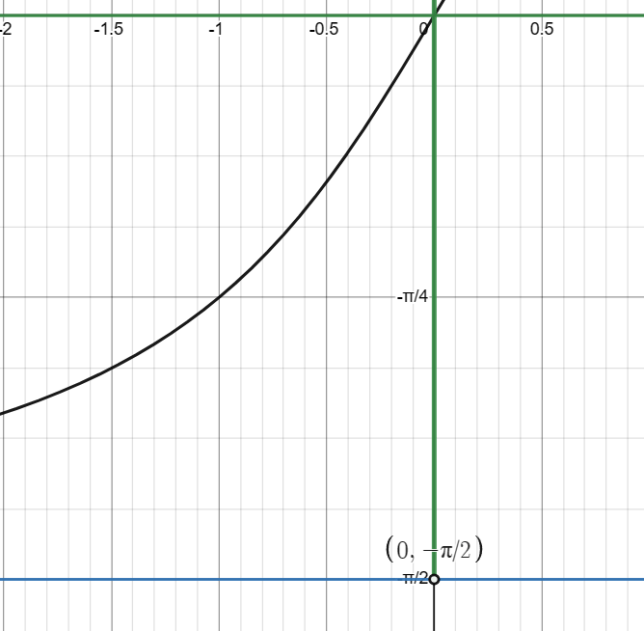
Unlock the Intricacies of the Inverse Tangent Function: tan⁻¹(x) 🧐
Domain and Range 🌐📊
The domain of tan⁻¹(x) is all real numbers, extending from -∞ to +∞. The range is limited to the open interval (-π/2, π/2).
Special Characteristics 🌟
Unlike tan(x), the function tan⁻¹(x) is defined for all real numbers and doesn’t have any vertical asymptotes. Instead, it has horizontal asymptotes at y = -π/2 and y = π/2.
Graph Behavior 📈
The graph of tan⁻¹(x) starts from the lower horizontal asymptote at y = -π/2, rises through zero at the origin, and asymptotically approaches the upper horizontal asymptote at y = π/2. The graph is continuous and smooth, without any breaks or sharp turns.
Key Insights 📚
The inverse tangent function, tan⁻¹(x), serves as an important tool in trigonometry and calculus, especially in problems dealing with angles and real-world applications like engineering and physics. Its continuous and smooth graph makes it much easier to work with compared to its counterpart, tan(x).