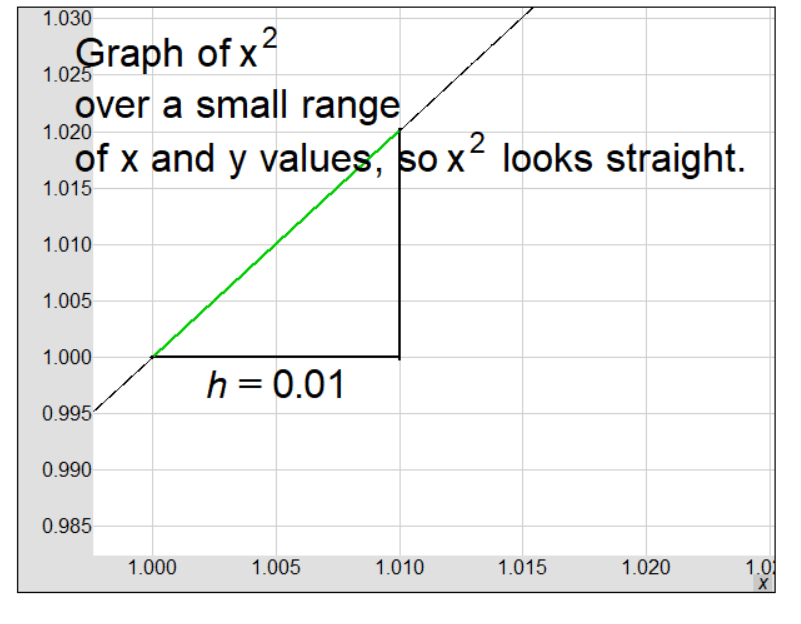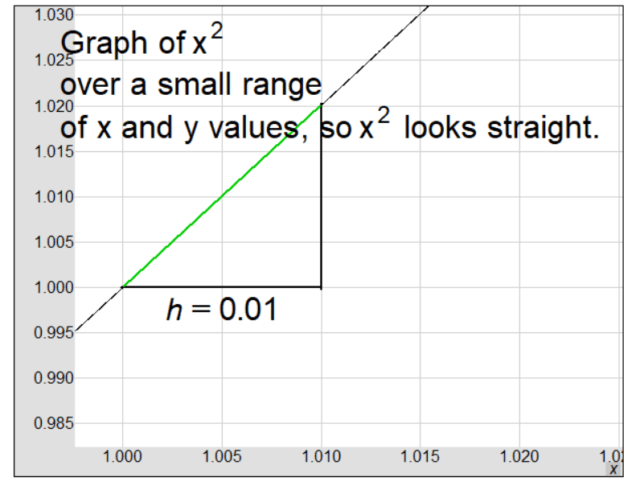
In this explanation, we look at the function \( f(x) = x^2 \) and explore its derivative from multiple angles.
- The formal derivative of \( f(x) = x^2 \) is \( f'(x) = 2x \).
- Evaluating this derivative at \( x = 1 \) gives us \( f'(1) = 2 \), indicating that the slope at \( x = 1 \) is 2 on \( f(x) = x^2 \).
- Notice in the graph, if we zoom in and find the difference quotient over a tiny interval (\( x = 1 \) to \( x = 1.01 \)), we get \( \frac{1.0201 – 1.0000}{1.0100 – 1.0000} = 2.000 \) which equals \( f'(1) \).
- In other words, \( f'(x) \approx \frac{f(1+h) – f(1)}{h} \) when \( h \) is tiny.