| \( x \) | Function | \( f(x) \) |
|---|---|---|
| -10000 | \( \frac{x^2 – 1}{x^2 + 1} \) | \( \frac{10000^2 – 1}{10000^2 + 1} \approx 0.9999 \) |
| -1000 | \( \frac{x^2 – 1}{x^2 + 1} \) | \( \frac{1000^2 – 1}{1000^2 + 1} \approx 0.9999 \) |
| 1000 | \( \frac{x^2 – 1}{x^2 + 1} \) | \( \frac{1000^2 – 1}{1000^2 + 1} \approx 0.9999 \) |
| 10000 | \( \frac{x^2 – 1}{x^2 + 1} \) | \( \frac{10000^2 – 1}{10000^2 + 1} \approx 0.9999 \) |
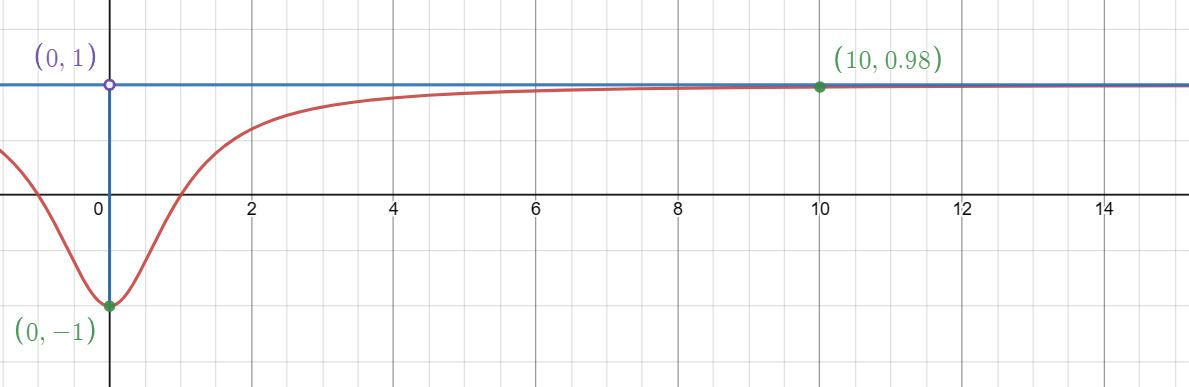
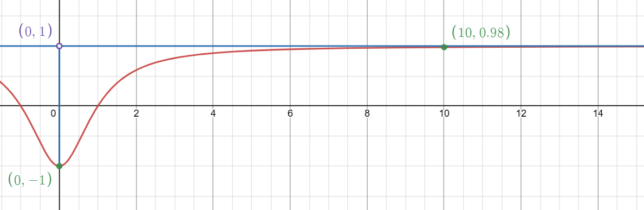
Explore the Complete Range of the Intriguing Mathematical Function f(x) = (x² – 1) / (x² + 1)
Unlock the full potential of understanding function ranges with our detailed exploration of the function f(x) = (x² – 1) / (x² + 1). One of the most fascinating aspects of this function is its range. The values that f(x) can take are remarkably restricted, revealing a captivating pattern.
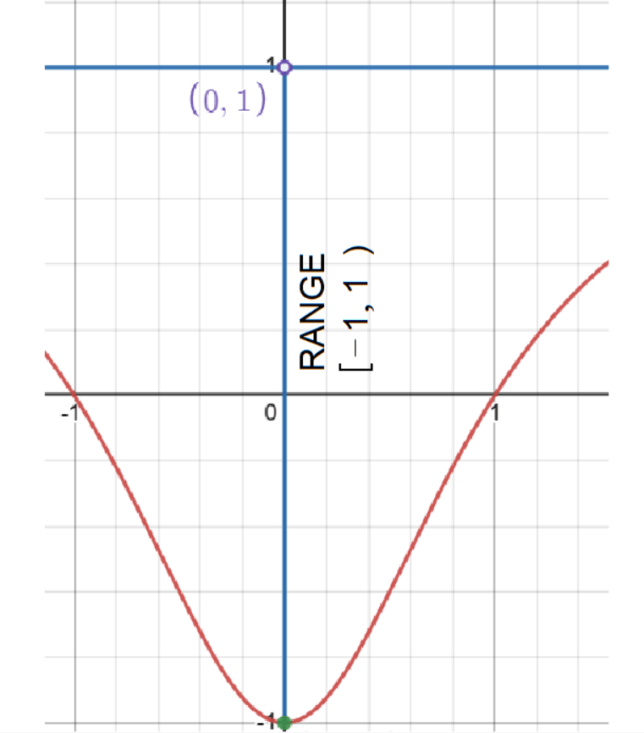
Range in Interval Notation
In interval notation, the range is expressed as [-1, 1). This means that the function includes the value -1 and approaches but never reaches 1.
Range in Set-Builder Notation
In set-builder notation, the range is { f(x) | -1 ≤ f(x) < 1 }. Here, it's evident that the value of -1 is included in the range while 1 is not.
Range in Inequality Form
The range in inequality form is -1 ≤ f(x) < 1. This indicates that f(x) can be as low as -1 (occurring when x = 0) and approach but not reach 1 as x moves towards positive or negative infinity.
Key Takeaway
The function f(x) = (x² – 1) / (x² + 1) offers a thrilling journey through mathematical analysis. Its range, confined between -1 and 1, provides a rich field for both novice learners and seasoned mathematicians to explore and understand the subtleties of function behavior.
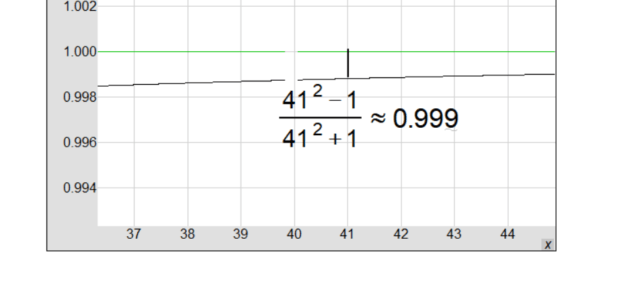
Zooming in on the Curious Behavior of f(x) = (x² – 1) / (x² + 1) at x=41 🧐
If you’ve ever wondered about the intricate details of mathematical functions, you’re in for a treat 🎉! Today, we’re zooming in 🕵️♀️ on a very specific point, x=41, in the function f(x) = (x² – 1) / (x² + 1).
Discover the Hidden Gap 👀
When you plot the graph of this function and look closely at x=41, you might initially think the function value is exactly 1. However, that’s not the case 🤔. If you zoom in 🧐 between the graph and y=1, you’ll discover there’s actually a tiny gap 🌌.
Why Does This Gap Matter? 🤔
This minuscule gap is a testament to the nuanced behavior of mathematical functions. While at a glance the function appears to touch y=1, it actually never does — it just gets infinitely close as x approaches infinity 📈. At x=41, the gap is extremely small but it’s there, a reminder that sometimes you have to look really closely to fully understand the subtleties of a function 🕵️♀️.
Key Takeaway 🗝
Mathematics is full of fascinating details that might not be apparent at first glance. To truly understand a function, sometimes you need to zoom in and observe its behavior at specific points. The tiny gap at x=41 in the function f(x) = (x² – 1) / (x² + 1) serves as a perfect example of these hidden mathematical treasures 🏆.