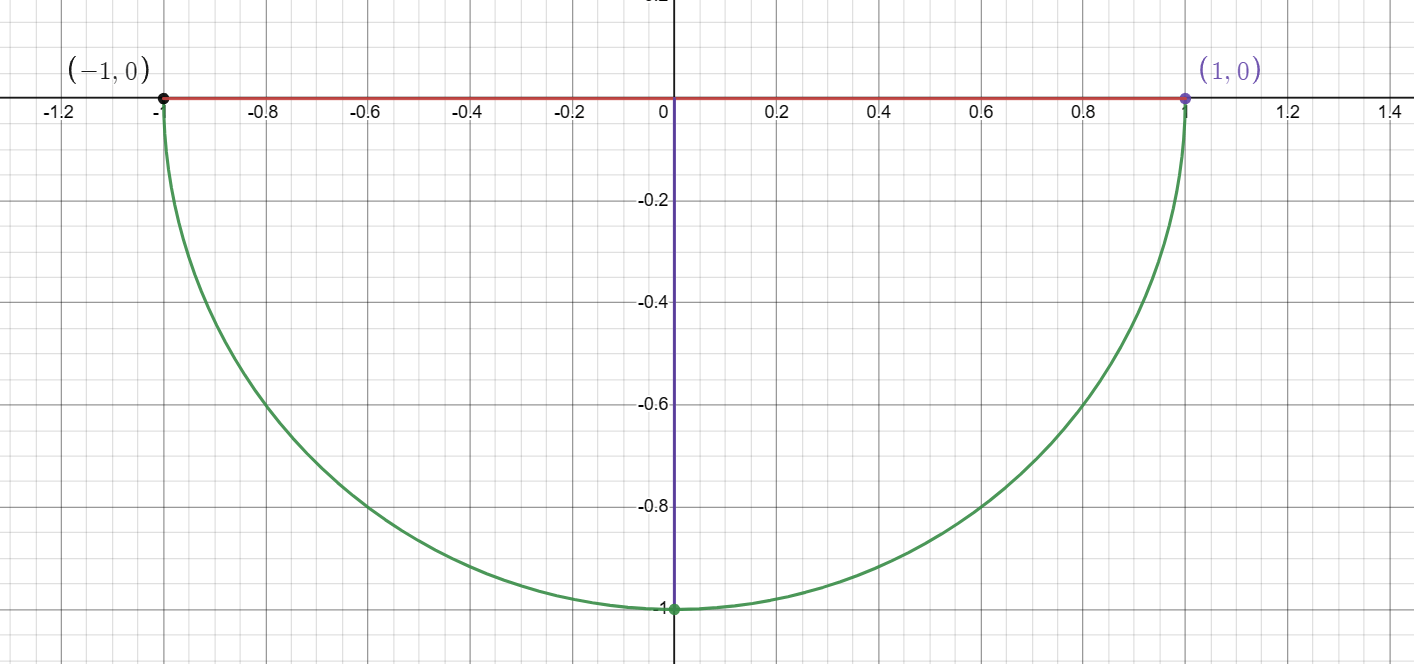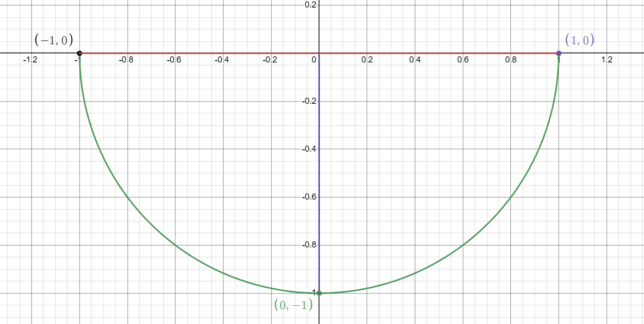
Master the Mystery: Unveil the Domain and Range of f(x) = -√(1 – x²)
Finding the Domain
Step 1: Identify the Radicand
The expression inside the square root is 1 – x².
Step 2: Set Constraints
For a square root to be defined, the expression inside must be greater than or equal to zero. Therefore, we get:
1 – x² ≥ 0
Step 3: Solve for x
We solve the inequality in the following steps:
- Move all terms to one side: 1 – x² ≥ 0
- Factor the inequality: (1 – x)(1 + x) ≥ 0
- Identify critical points: x = 1 and x = -1
- Test intervals: -1 ≤ x ≤ 1
We find that the inequality 1 – x² ≥ 0 is true when -1 ≤ x ≤ 1.
Step 4: State the Domain
Therefore, the domain of f(x) = -√(1 – x²) is -1 ≤ x ≤ 1.
Finding the Range
Step 1: Behavior of the Function
The square root function √x outputs non-negative values. The negative sign in front of the square root changes these to non-positive values.
Step 2: Minimum and Maximum of Radicand
The smallest value of 1 – x² is 0 (when x = 1 or x = -1), and the largest value is 1 (when x = 0).
Step 3: Apply Negative Square Root
The square root of these minimum and maximum values are:
- -√0 = 0
- -√1 = -1
Step 4: State the Range
The function will output values between 0 and -1, inclusive. Thus, the range of f(x) = -√(1 – x²) is -1 ≥ f(x) ≥ 0.
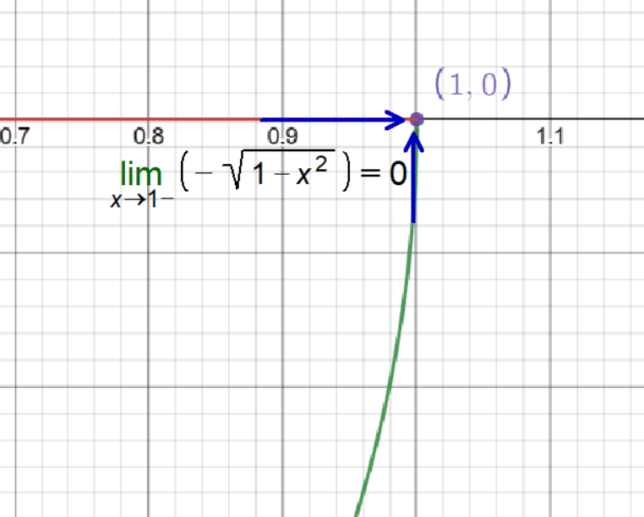
Crack the Code: Understanding the Limit of f(x) = -√(1 – x²) as x Approaches 1 from the Left
Step 1: Identify the Function and Point of Interest
The function under consideration is f(x) = -√(1 – x²), and the point we are interested in is x = 1.
Step 2: Observe the Function’s Behavior
As x gets closer to 1 from the left side (meaning x is less than but very close to 1), the expression 1 – x² gets closer and closer to zero.
Step 3: Evaluate the Limit
The square root of zero is zero. However, since there is a negative sign in front of the square root, the function value also approaches zero but stays at zero.
Step 4: State the Limit
Therefore, the limit of f(x) = -√(1 – x²) as x approaches 1 from the left side is 0.
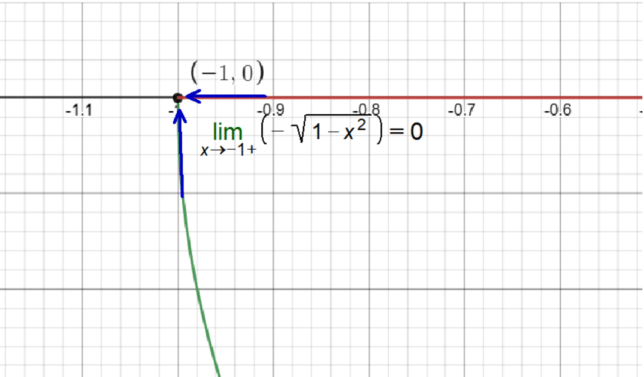
Demystifying Limits: Understanding the Limit of f(x) = -√(1 – x²) as x Approaches -1 from the Right
Step 1: Identify the Function and Point of Interest
The function we’re looking at is f(x) = -√(1 – x²), and the point of interest is x = -1.
Step 2: Observe the Function’s Behavior
As x approaches -1 from the right, the expression 1 – x² gets increasingly close to zero.
Step 3: Evaluate the Limit
The square root of zero is zero, and the negative sign in front of the square root keeps it at zero.
Step 4: State the Limit
Therefore, the limit of f(x) = -√(1 – x²) as x approaches -1 from the right is 0.