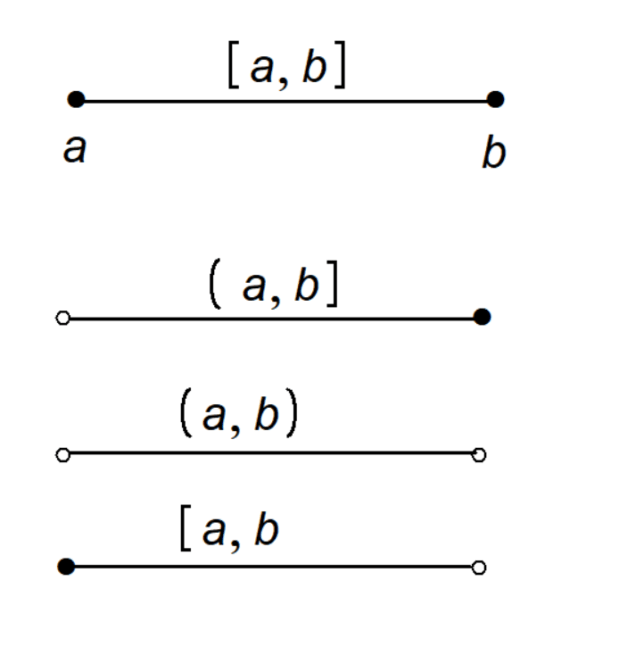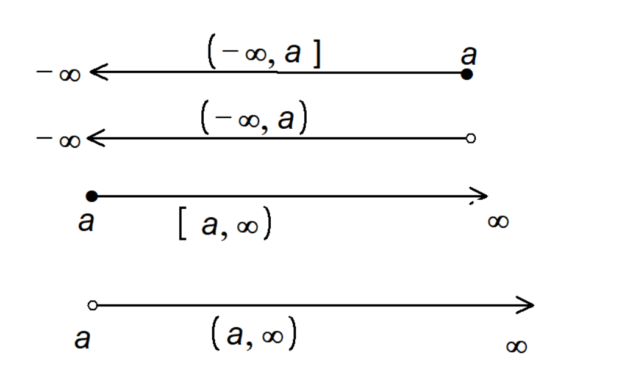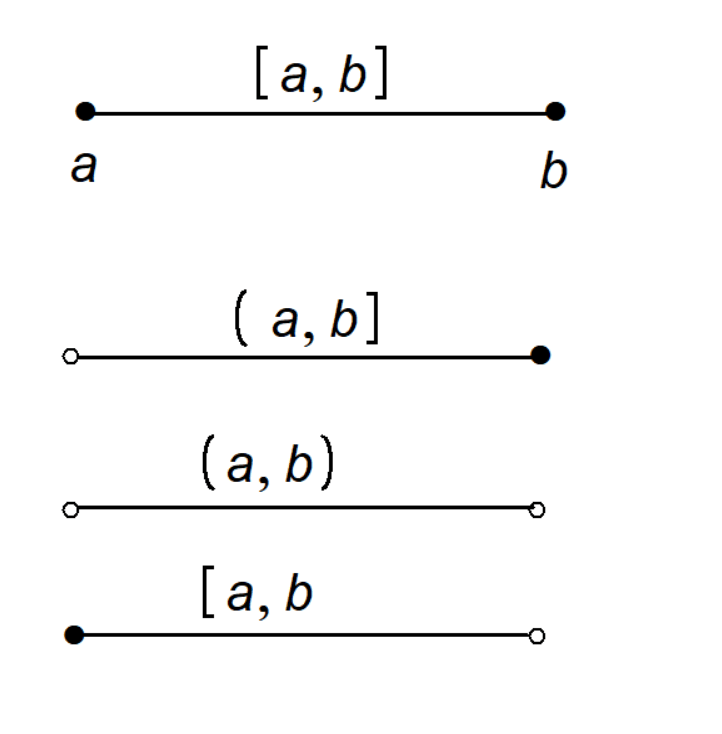Closed Interval [a, b]
In a closed interval, both endpoints ‘a’ and ‘b’ are included. The square brackets [ ] signify that the endpoints are part of the interval. For example, [1, 5] includes all numbers from 1 to 5, including 1 and 5 themselves.
Open Interval (a, b)
In an open interval, both endpoints ‘a’ and ‘b’ are excluded. The parentheses ( ) indicate that the endpoints are not part of the interval. For example, (1, 5) includes all numbers greater than 1 and less than 5, but not 1 and 5 themselves.
Half-Open or Half-Closed Interval [a, b) or (a, b]
In a half-open or half-closed interval, one endpoint is included while the other is excluded. The combination of a square bracket [ ] and a parenthesis ( ) indicates which endpoint is included and which is excluded.
- [a, b): Includes ‘a’ but excludes ‘b’
- (a, b]: Excludes ‘a’ but includes ‘b’
Infinite Intervals
These intervals extend infinitely in one or both directions. The symbol ‘∞’ represents infinity, indicating that the interval has no upper or lower bound.
- (a, ∞): All numbers greater than ‘a’
- [a, ∞): All numbers greater than or equal to ‘a’
- (-∞, a): All numbers less than ‘a’
- (-∞, a]: All numbers less than or equal to ‘a’
- (-∞, ∞): All real numbers
Singleton Interval [a, a] or {a}
This is an interval that contains only one element. It is denoted as [a, a] or simply {a}. The square brackets or curly braces indicate that the interval contains just the single number ‘a’.
Empty Interval
An interval that contains no elements is called an empty interval. It is usually denoted by an empty set symbol ‘∅’ or as (a, a) where ‘a’ is any real number. This signifies that the interval has no elements.
Closed Interval [a, b]
In a closed interval, both endpoints are included. Example: [2, 4] includes all numbers from 2 to 4, including 2 and 4.
Open Interval (a, b)
In an open interval, both endpoints are excluded. Example: (2, 4) includes all numbers greater than 2 and less than 4.
Half-Open or Half-Closed Interval [a, b) or (a, b]
In a half-open or half-closed interval, one endpoint is included while the other is excluded.
- [2, 4): Includes 2 but excludes 4.
- (2, 4]: Excludes 2 but includes 4.
Infinite Intervals
These intervals extend infinitely in one or both directions.
- (2, ∞): Includes all numbers greater than 2.
- (-∞, 2): Includes all numbers less than 2.
Singleton Interval [a, a] or {a}
This is an interval that contains only one element. Example: [3, 3] or {3} includes just the number 3.
Empty Interval
An interval that contains no elements is called an empty interval. It is usually denoted by an empty set symbol ‘∅’.
Example: (3, 3) = ∅