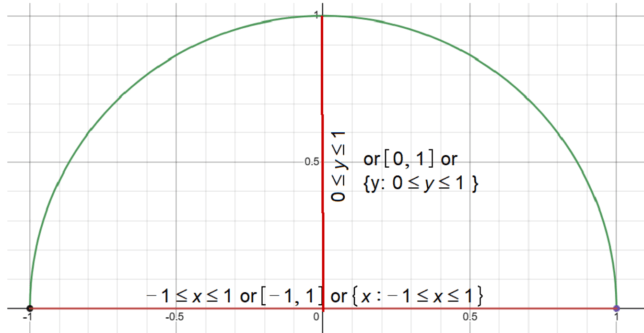
Finding the Domain of f(x) = √(1 – x²)
To find the domain of the function f(x) = √(1 – x²), you need to identify the set of all real numbers x for which the function is defined.
Step 1: Identify the Radicand
The expression inside the square root is 1 – x².
Step 2: Set Constraints
For a square root to be defined, the expression inside must be greater than or equal to zero. Therefore:
1 – x² ≥ 0
Step 3: Solve for x
To find the values of x that satisfy the inequality, solve for x:
- Move all terms to one side: 1 – x² ≥ 0
- Factor the equation: (1 – x)(1 + x) ≥ 0
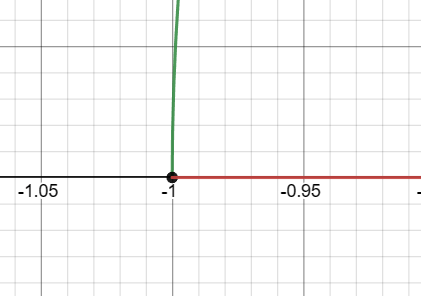
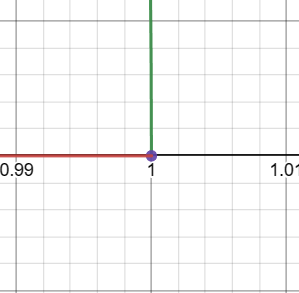
- Identify critical points: x = 1 and x = -1
- Test intervals: x < -1, -1 < x < 1, and x > 1
We find that only -1 ≤ x ≤ 1 satisfies the inequality 1 – x² ≥ 0.
Step 4: State the Domain
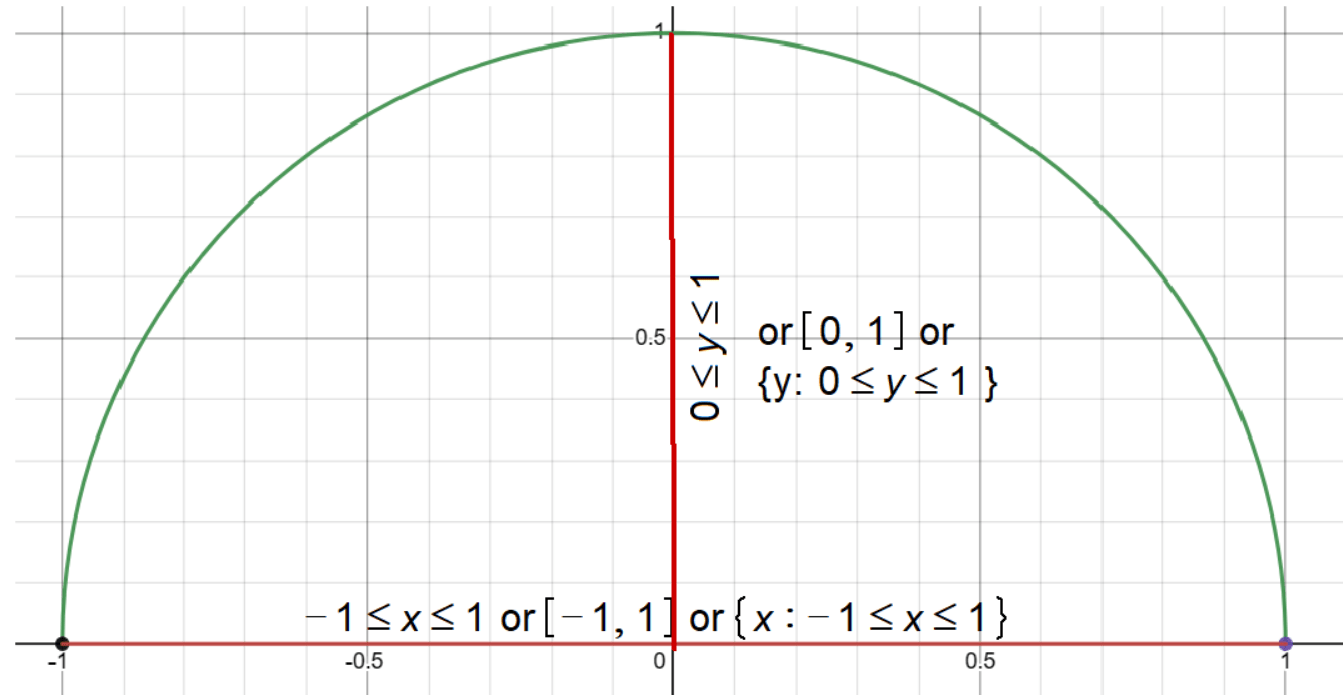
The domain of f(x) = √(1 – x²) is -1 ≤ x ≤ 1.
Finding the Range of f(x) = √(1 – x²)
To find the range of the function f(x) = √(1 – x²), you need to identify the set of all possible output values f(x).
Step 1: Identify Domain Constraints
We already know that -1 ≤ x ≤ 1.
Step 2: Identify the Function’s Behavior
The square root function √x produces non-negative values for a non-negative input.
Step 3: Look at the Radicand 1 – x²
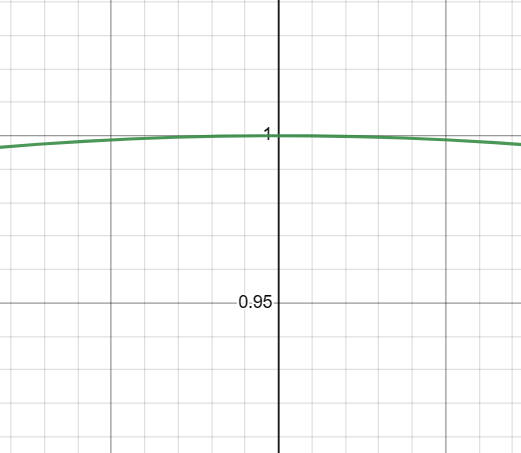
The smallest value of 1 – x² is zero, and the largest value is 1.
Step 4: Apply Square Root
When you take the square root of these values, you get √0 = 0 and √1 = 1.
Step 5: State the Range
The function will take on all values between 0 and 1, inclusive. Hence, the range of f(x) = √(1 – x²) is 0 ≤ f(x) ≤ 1.