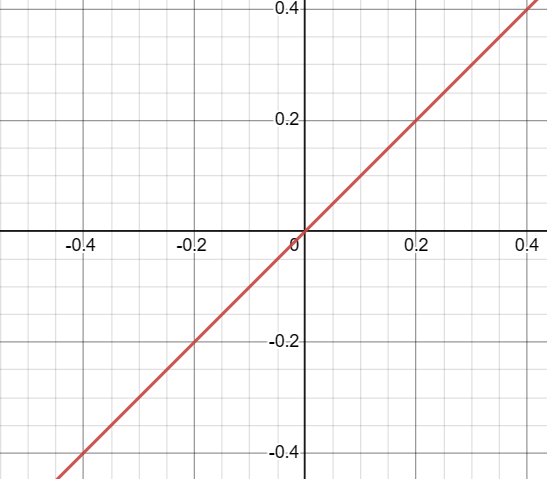
The function f(x) = x behaves linearly around x = 0. Specifically, as you approach 0 from either the left or the right, the function approaches 0 as well.
- As x approaches 0 from the left, f(x) approaches 0 from below.
- As x approaches 0 from the right, f(x) approaches 0 from above.
This behavior indicates that the root at x = 0 has a multiplicity of 1. In general, the multiplicity of a root tells us how many times that particular root appears in the function’s equation. For f(x) = x, the root at x = 0 appears only once, confirming its multiplicity of 1.
Because the root has a multiplicity of 1, the graph of the function crosses the x-axis at x = 0 without “bouncing” or “flattening out.”
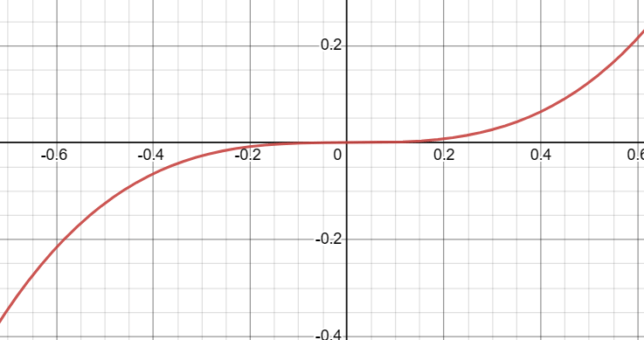
The function f(x) = x³ behaves cubically around x = 0. As you approach 0 from either the left or the right, the function also approaches 0.
- As x approaches 0 from the left, f(x) approaches 0 from below.
- As x approaches 0 from the right, f(x) approaches 0 from above.
This behavior indicates that the root at x = 0 has a multiplicity of 3. The multiplicity of a root tells us how many times that particular root appears in the function’s equation. For f(x) = x³, the root at x = 0 appears three times, confirming its multiplicity of 3.
Because the root has a multiplicity of 3, the graph of the function crosses the x-axis at x = 0 without “bouncing,” but it does “flatten out” momentarily as it crosses.
Calculations Close to x=0 for x³
| x Value | f(x) = x³ |
|---|---|
| -0.1 | -0.001 |
| -0.01 | -0.000001 |
| -0.001 | -0.000000001 |
| 0 | 0 |
| 0.001 | 0.000000001 |
| 0.01 | 0.000001 |
| 0.1 | 0.001 |
This table shows how f(x) = x³ behaves as x approaches 0 from both the left and the right.
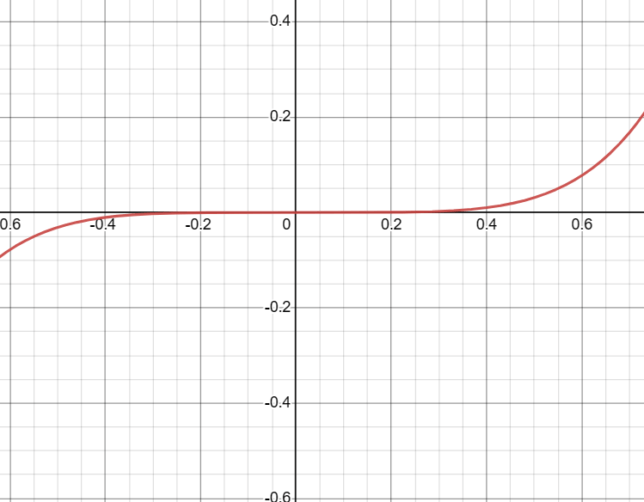
The function f(x) = x⁵ behaves in a quintic manner around x = 0. As you approach 0 from either the left or the right, the function also approaches 0.
- As x approaches 0 from the left, f(x) approaches 0 from below.
- As x approaches 0 from the right, f(x) approaches 0 from above.
This behavior indicates that the root at x = 0 has a multiplicity of 5. The multiplicity of a root tells us how many times that particular root appears in the function’s equation. For f(x) = x⁵, the root at x = 0 appears five times, confirming its multiplicity of 5.
Because the root has a multiplicity of 5, the graph of the function crosses the x-axis at x = 0 without “bouncing,” but it does “flatten out” momentarily as it crosses. The flattening is more pronounced than in the cubic case.
Calculations Close to x=0 for x⁵
| x Value | f(x) = x⁵ |
|---|---|
| -0.1 | -0.00001 |
| -0.01 | -0.0000000001 |
| -0.001 | -0.000000000000001 |
| 0 | 0 |
| 0.001 | 0.000000000000001 |
| 0.01 | 0.0000000001 |
| 0.1 | 0.00001 |
This table shows how f(x) = x⁵ behaves as x approaches 0 from both the left and the right.
General Behavior Close to x=0 for xⁿ (When n is Odd)
For any odd integer value of n, the function f(x) = xⁿ will behave in a similar manner around x = 0:
- As x approaches 0 from the left, f(x) approaches 0 from below.
- As x approaches 0 from the right, f(x) approaches 0 from above.
This behavior indicates that the root at x = 0 has a multiplicity of n. The multiplicity of a root tells us how many times that particular root appears in the function’s equation.
Because the root has a multiplicity of n, the graph of the function will cross the x-axis at x = 0 without “bouncing,” but it will “flatten out” momentarily as it crosses. The higher the value of n, the more pronounced the flattening will be.
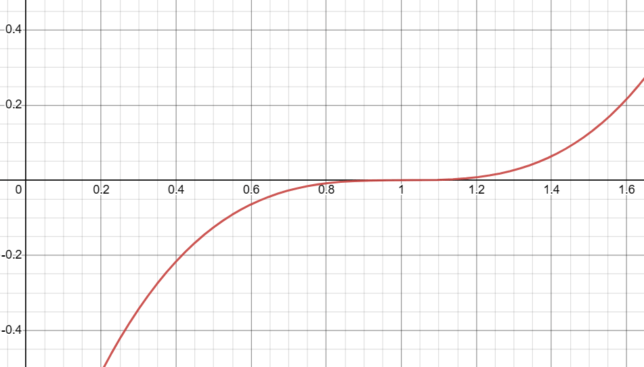
Behavior Close to x=1 for (x-1)³ and Its Relationship with x³
The function f(x) = (x-1)³ behaves cubically around x = 1, similar to how f(x) = x³ behaves around x = 0.
- As x approaches 1 from the left, f(x) approaches 0 from below.
- As x approaches 1 from the right, f(x) approaches 0 from above.
This behavior indicates that the root at x = 1 has a multiplicity of 3, just like the root at x = 0 for f(x) = x³.
The graph of f(x) = (x-1)³ is essentially the graph of f(x) = x³ shifted one unit to the right. This shift does not affect the multiplicity of the root or the general shape of the graph near the root; it simply moves the location of the root from x = 0 to x = 1.
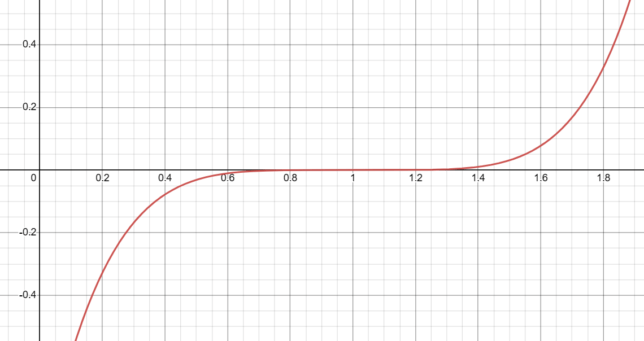
Behavior Close to x=1 for (x-1)⁵ and Its Relationship with x⁵
The function f(x) = (x-1)⁵ behaves in a quintic manner around x = 1, similar to how f(x) = x⁵ behaves around x = 0.
- As x approaches 1 from the left, f(x) approaches 0 from below.
- As x approaches 1 from the right, f(x) approaches 0 from above.
This behavior indicates that the root at x = 1 has a multiplicity of 5, just like the root at x = 0 for f(x) = x⁵.
The graph of f(x) = (x-1)⁵ is essentially the graph of f(x) = x⁵ shifted one unit to the right. This shift does not affect the multiplicity of the root or the general shape of the graph near the root; it simply moves the location of the root from x = 0 to x = 1.
Comparing xⁿ and (x-a)ⁿ for Odd Values of n
For any odd integer n, the functions f(x) = xⁿ and g(x) = (x-a)ⁿ share similar characteristics but are shifted along the x-axis.
- Both functions will have a root with a multiplicity of n.
- Both functions will “flatten out” momentarily as they cross the x-axis, with the degree of flattening depending on the value of n.
- Both functions will approach 0 from below as x approaches the root from the left and from above as x approaches the root from the right.
The primary difference is the location of the root:
- For f(x) = xⁿ, the root is at x = 0.
- For g(x) = (x-a)ⁿ, the root is at x = a.
In summary, g(x) = (x-a)ⁿ is a horizontal shift of f(x) = xⁿ, moving the graph a units to the right. This shift does not affect the multiplicity of the root or the general shape of the graph near the root.
