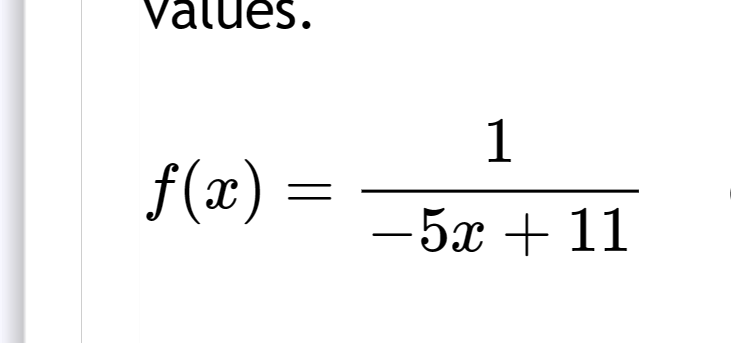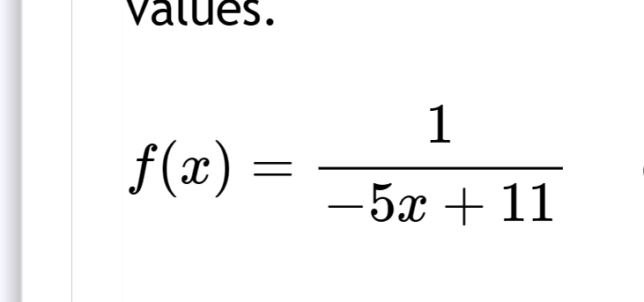
Function: f(x) = 1 / (-5x + 11)
Step 1: Identify the Forbidden Value
The denominator of the function can’t be zero because division by zero is undefined. To find the values that would make the denominator zero, we set -5x + 11 equal to zero.
Step 2: Solve for Forbidden Value
We solve -5x + 11 = 0 by isolating x. Adding 5x to both sides and then dividing by -5, we determine that x = 11 / 5 or x = 2.2. These values are the ones that x cannot be to avoid division by zero.
Step 3: Express the Domain
Inequality Form:
x < 2.2 or x > 2.2. In this form, it’s clear that x can be any number less than 2.2 or any number greater than 2.2, but not equal to 2.2.
Interval Form:
(-∞, 2.2) ∪ (2.2, ∞). We use (-∞, 2.2) to indicate all numbers less than 2.2, and (2.2, ∞) to indicate all numbers greater than 2.2. The ‘∪’ symbol combines these two sets.
Set Builder Form:
{x | x is a real number, x is not equal to 2.2}. In this form, we specify that x belongs to the set of real numbers, and we exclude the value 2.2 using ‘is not equal to’.
Translation of Symbols:
‘∪’ means ‘union’, which combines sets. ‘is a real number’ indicates the type of numbers x can be, and ‘is not equal to’ explicitly excludes 2.2 from the set of allowed values.
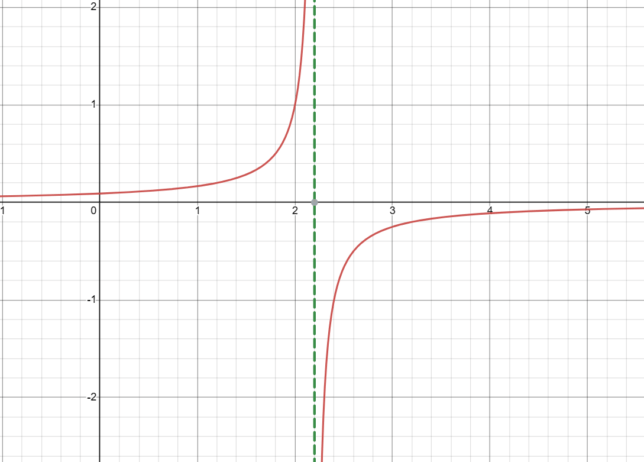
Let’s calculate f(2.2) for the function f(x) = 1 / (-5x + 11).
Substituting x = 2.2 into the function:
f(2.2) = 1 / (-5 * 2.2 + 11)
Now, let’s compute the denominator:
-5 * 2.2 + 11 = -11 + 11 = 0
The denominator becomes zero, and in mathematics, division by zero is undefined.
Therefore, f(2.2) is undefined or “does not exist.”
This occurs because at x = 2.2, the function f(x) has a vertical asymptote, and its values approach infinity as x gets closer to 2.2 from either the left or right side, but it never reaches a specific value at that point.