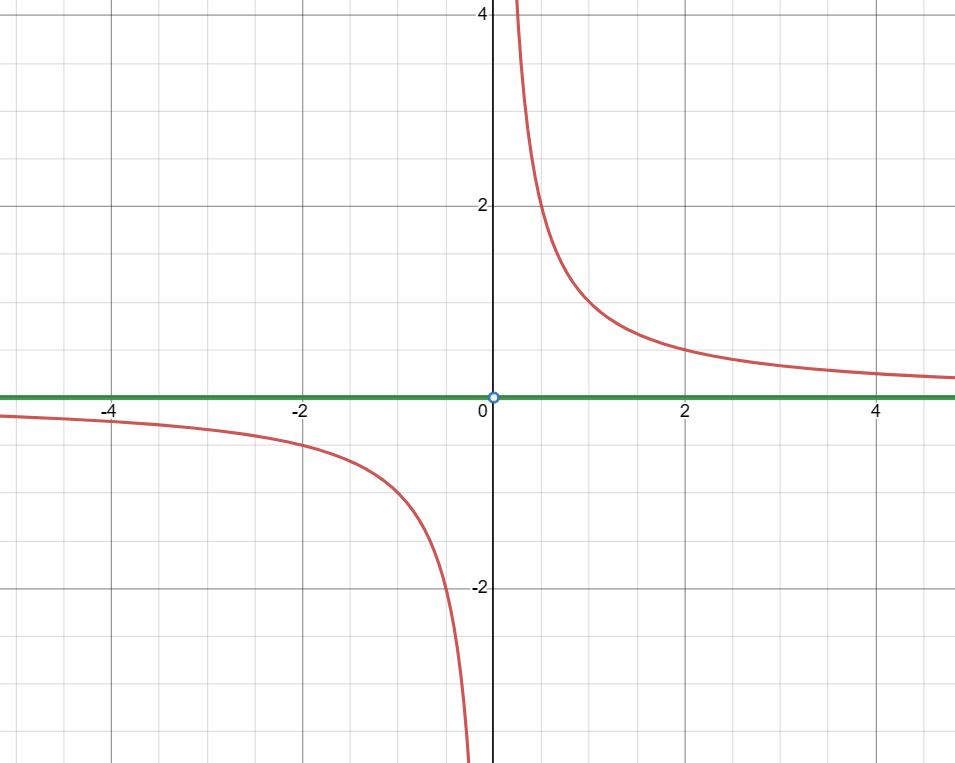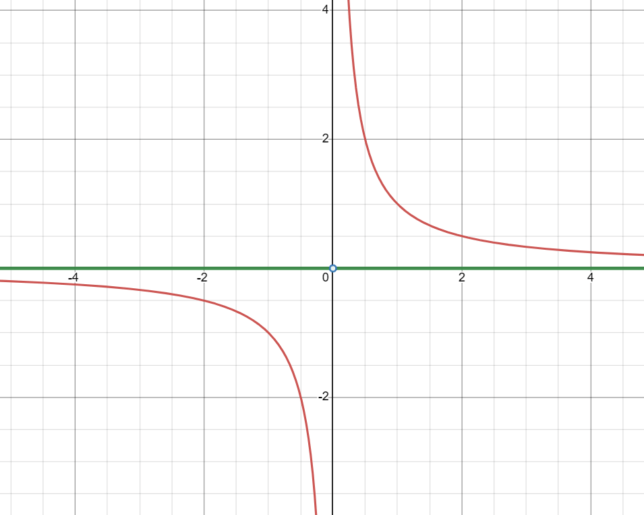
Domain in Inequality Form: x < 0 or x > 0 (The domain is all x such that x is less than 0 or x is greater than 0)
Domain in Interval Notation: (-∞, 0) ∪ (0, ∞) (The domain is from negative infinity to 0, union, from 0 to positive infinity)
Domain in Set-builder Notation: { x ∈ ℝ : x ≠ 0 } (The domain is the set of all x in the real numbers such that x is not equal to 0)
| x | 1/x |
|---|---|
| 0.1 | 10 |
| 0.01 | 100 |
| 0.001 | 1000 |
| 0.0001 | 10000 |
Summary: As x approaches zero from the positive side, the value of 1/x increases rapidly towards positive infinity. The closer x gets to zero, the larger 1/x becomes, illustrating the concept of a vertical asymptote at x=0.
| x | 1/x |
|---|---|
| -0.1 | -10 |
| -0.01 | -100 |
| -0.001 | -1000 |
| -0.0001 | -10000 |
Summary: As x approaches zero from the negative side, the value of 1/x decreases rapidly towards negative infinity. The closer x gets to zero, the larger the magnitude of 1/x becomes in the negative direction, illustrating the concept of a vertical asymptote at x=0.
| x | 1/x |
|---|---|
| 10 | 0.1 |
| 100 | 0.01 |
| 1000 | 0.001 |
| 10000 | 0.0001 |
Summary: As x approaches infinity, the value of 1/x approaches zero from the positive side. The larger x becomes, the closer 1/x gets to zero, illustrating the concept of a horizontal asymptote at y=0.
| x | 1/x |
|---|---|
| -10 | -0.1 |
| -100 | -0.01 |
| -1000 | -0.001 |
| -10000 | -0.0001 |
Summary: As x approaches negative infinity, the value of 1/x approaches zero from the negative side. The more negative x becomes, the closer 1/x gets to zero, illustrating the concept of a horizontal asymptote at y=0.