Domain of the Function |2x + 1|/(2x + 1)
- Interval Notation: (-∞, -1/2) ∪ (-1/2, ∞)
- Set-Builder Notation: { x ∈ R : x ≠ -1/2 }
- In Words: All real numbers except x = -1/2
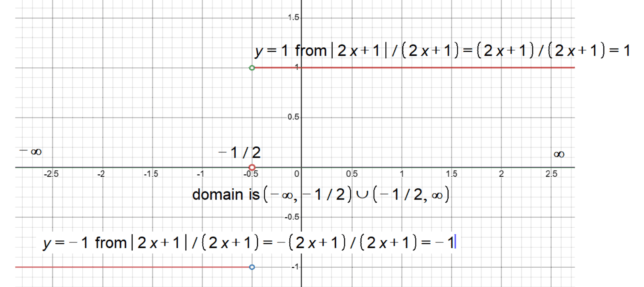
Deep Dive into the Limit of |2x + 1| / (2x + 1) as x Nears -1/2
Approaching from the Right-Hand Side (RHS):
When we consider values of x that are just a little bit greater than -1/2, the expression inside the absolute value, 2x + 1, will be positive. So, the absolute value |2x + 1| simplifies to 2x + 1. Because of this, the whole function becomes 1, as both the numerator and denominator are identical and cancel each other out.
Approaching from the Left-Hand Side (LHS):
However, when we consider values of x that are just a little bit less than -1/2, the expression 2x + 1 is negative. The absolute value then changes the sign, making it -(2x + 1). The function then simplifies to -1 because the numerator becomes the negative of the denominator.
Final Conclusion:
Because the function approaches 1 from the right and -1 from the left as x gets closer to -1/2, the limit does not exist. The function has different behaviors depending on whether you approach -1/2 from the right or the left, making it discontinuous at that point.

