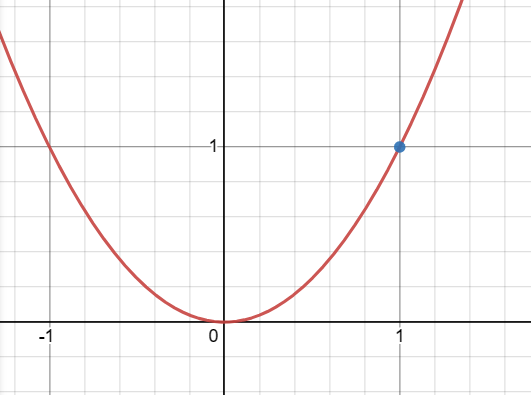
Approximating the Derivative of \( f(x) = x^2 \) at \( x = 1 \)
We want to find the slope around the point \( (1, 1) \) for the function \( f(x) = x^2 \).
We’ll use the average rate of change formula:
\[ \text{Average Rate of Change} = \frac{f(x_2) – f(x_1)}{x_2 – x_1} \]
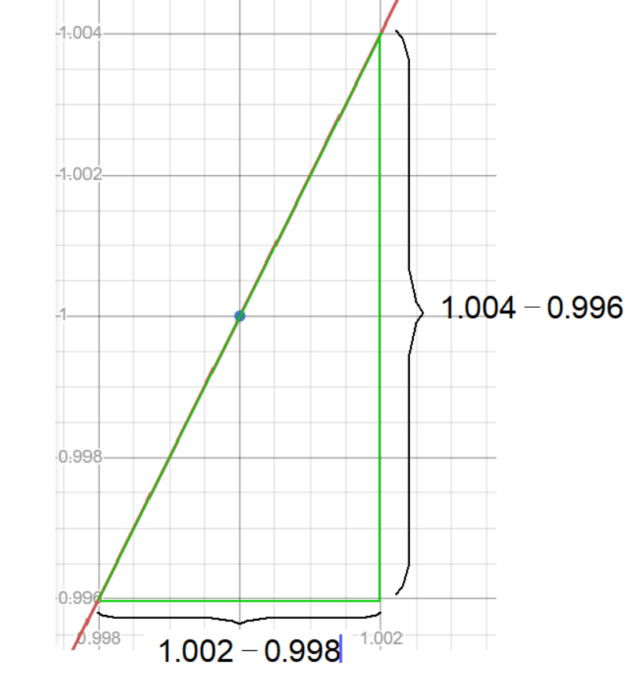
Here, \( x_1 = 0.998 \) and \( x_2 = 1.002 \).
Step 1: Calculate \( f(x_1) \) and \( f(x_2) \)
\[ f(x_1) = 0.998^2 = 0.996004 \]
\[ f(x_2) = 1.002^2 = 1.004004 \]
Step 2: Use the Average Rate of Change Formula
\[ \text{Average Rate of Change} = \frac{1.004004 – 0.996004}{1.002 – 0.998} \]
\[ \text{Average Rate of Change} = \frac{0.008}{0.004} \]
\[ \text{Average Rate of Change} = 2 \]
Conclusion
The average rate of change, which approximates the derivative of \( f(x) = x^2 \) at \( x = 1 \), is 2.
