Unlocking the Secrets of the Limit: A Joyful Dive into (3x + 1) / (x + 4) as x Approaches 5!

Unlocking the Secrets of the Limit: A Joyful Dive into (3x + 1) / (x + 4) as x Approaches 5!

Ever wondered what happens to the function (3x + 1) / (x + 4) as x gets closer and closer to 5? You’re in for a treat! Let’s unravel this mathematical mystery together!

Step 1: A Quick Look for Direct Substitution

First up, let’s find out if the function gives us a nice, neat answer when we plug in x = 5.

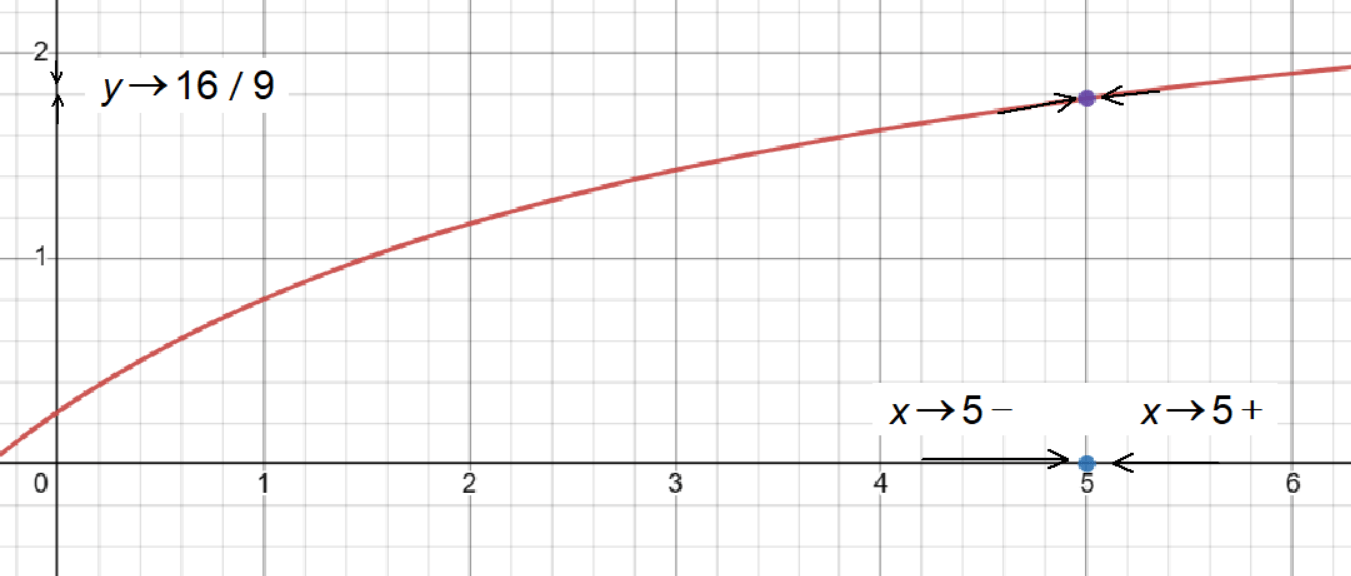
lim(x → 5) (3x + 1) / (x + 4)

Step 2: The Magic of Direct Substitution

Here comes the fun part! Let’s substitute x = 5 and see what we get:

(3 × 5 + 1) / (5 + 4) = 16 / 9

Step 3: Is Our Function Playing Nice? (Checking Continuity)

Great news! The function (3x + 1) / (x + 4) is smooth sailing at x = 5. It’s continuous!

Step 4: Drumroll, Please! Confirming the Limit Value

We’re almost there! Since everything is looking good, our limit is simply the function’s value at x = 5!

lim(x → 5) (3x + 1) / (x + 4) = 16 / 9

Voila! We’ve just discovered that the limit of (3x + 1) / (x + 4) as x zooms in on 5 is a fabulous 16 / 9!

And there you have it! A thrilling journey that took us into the heart of this fascinating function. We’ve not only solved a math problem, but we’ve also had a blast doing it!