Unveil the Secrets of the Enigmatic Graph: 1/(x-1) – 2
Soviet Joke: In Soviet Russia, function graphs you! 🇷🇺
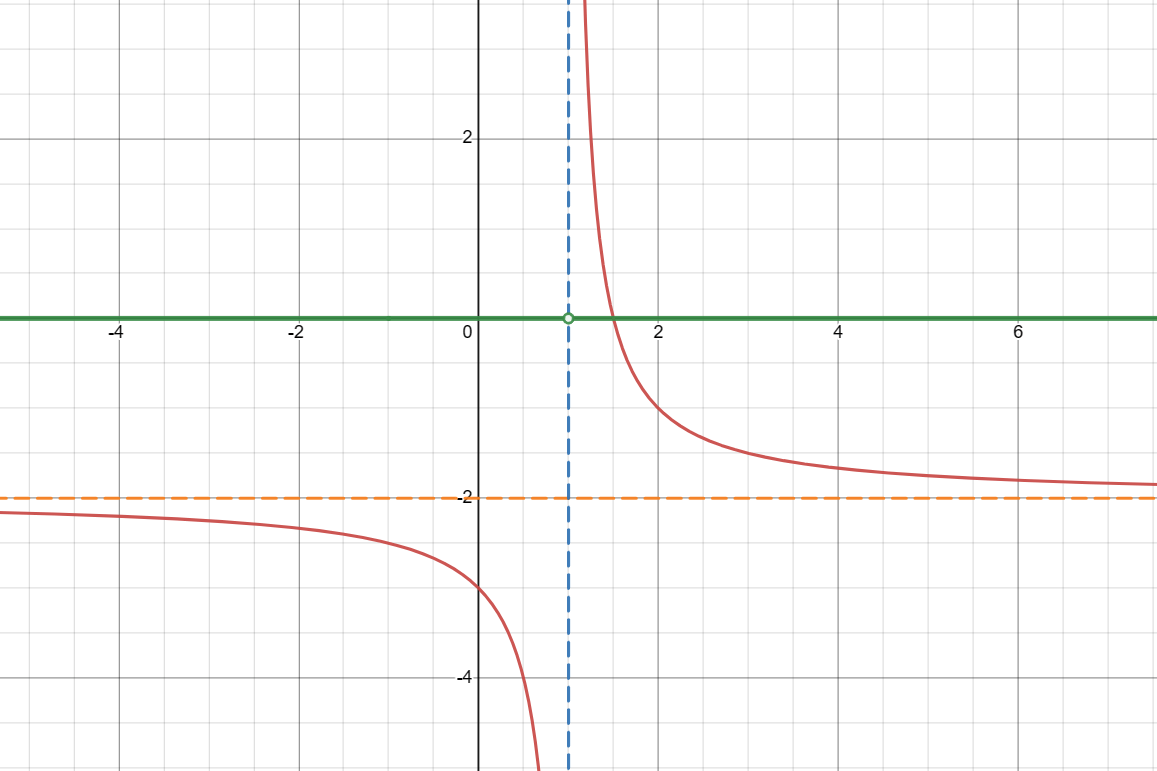
Cracking the Code: Why x = 1 is the Vertical Asymptote
- Identify the Denominator: In the function 1/(x-1) – 2, the denominator is x-1.
- Set the Denominator Equal to Zero: To find where the function is undefined, set the denominator x-1 equal to zero.
- Solve for x: Solving the equation x-1 = 0 gives x = 1.
- Vertical Asymptote: Since the function becomes undefined at x = 1, this is where the vertical asymptote occurs.
Unlocking the Mysteries: Additional Graph Features
- Horizontal Asymptote: The graph has a horizontal asymptote at y = -2. As x moves towards positive or negative infinity, the graph approaches this line but never actually reaches it.
- Quadrants: The graph is located in the 2nd and 4th quadrants. This is because the function is shifted two units down.
- End Behavior: As x approaches 1 from the left, the function value (y) dives towards negative infinity. As x approaches 1 from the right, the function value (y) soars towards positive infinity.
- Curve Shape: The graph is hyperbolic, meaning it has a curve that gets closer and closer to the asymptotes but never actually touches them.
- Shift: Compared to the graph of 1/x, this graph is shifted one unit to the right and two units down, due to the “-1” in the denominator and the “-2” subtracted from the function.