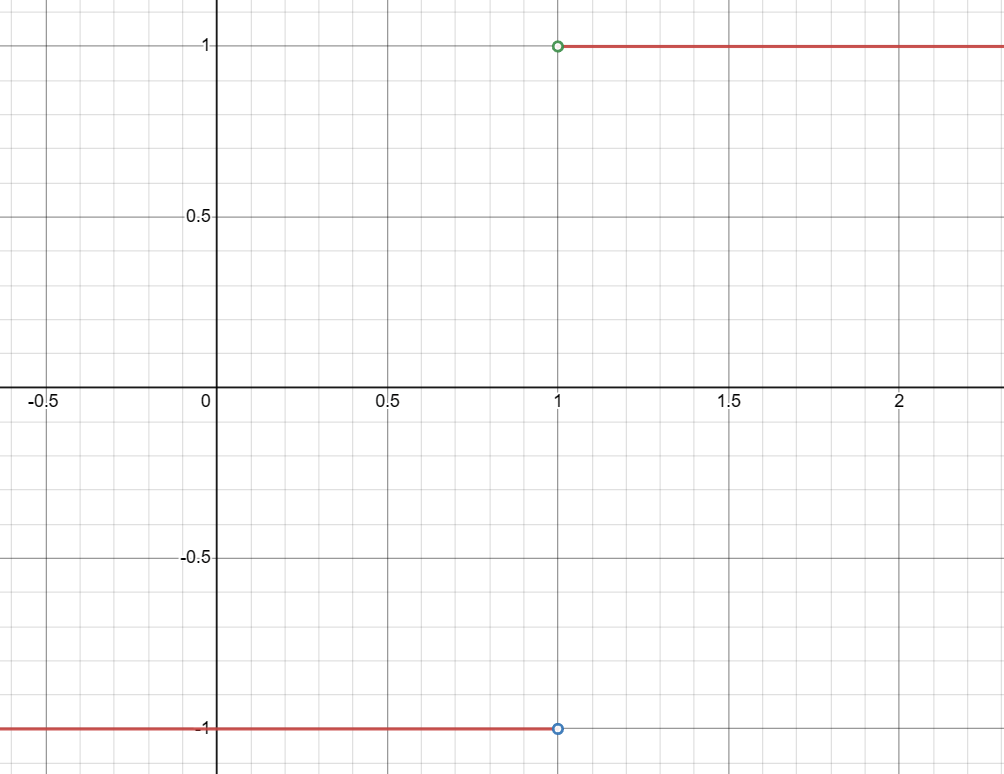
Final Result: Does the Limit of |x-1|/(x-1) as x Approaches 1 Exist?
The limit does not exist. Below is the complete step-by-step explanation:
- Case for x > 1: In this case, |x – 1| = x – 1. Therefore, the limit becomes lim(x → 1) (x – 1)/(x – 1) which simplifies to 1.
- Case for x < 1: Here, |x - 1| = -(x - 1). So the limit becomes lim(x → 1) -(x - 1)/(x - 1) which simplifies to -1.
- Graph Analysis: The graph consists of two separate pieces, one for x > 1 and another for x < 1. Additionally, the graph has holes at the points (1, 1) and (1, -1), signifying that the function is undefined at x = 1.
Since the limit approaches different values for x > 1 and x < 1, and the function is undefined at x = 1, the overall limit as x approaches 1 does not exist.
Behavior of |x-1|/(x-1) as x Approaches 1 from the RHS
| x | |x-1|/(x-1) |
|---|---|
| 1.1 | 1 |
| 1.01 | 1 |
| 1.001 | 1 |
| 1.0001 | 1 |
| 1.00001 | 1 |
The table shows that as x gets closer to 1 from the right-hand side, the value of |x-1|/(x-1) approaches 1.
Behavior of |x-1|/(x-1) as x Approaches 1 from the LHS
| x | Substituted Fraction (|x-1|/(x-1)) | Result of |x-1|/(x-1) |
|---|---|---|
| 0.9 | |0.9-1|/(0.9-1) | -1 |
| 0.99 | |0.99-1|/(0.99-1) | -1 |
| 0.999 | |0.999-1|/(0.999-1) | -1 |
| 0.9999 | |0.9999-1|/(0.9999-1) | -1 |
| 0.99999 | |0.99999-1|/(0.99999-1) | -1 |
The table shows that as x gets closer to 1 from the left-hand side, the value of |x-1|/(x-1) approaches -1.
Domain of the Function |x – 1|/(x – 1)
- Interval Notation: (-∞, 1) ∪ (1, ∞)
- Set-Builder Notation: { x ∈ R : x ≠ 1 }
- In Words: All real numbers except x = 1