Exploring the Shifted Circle: Understanding the Domain and Range of (x – 1)² + y² = 1
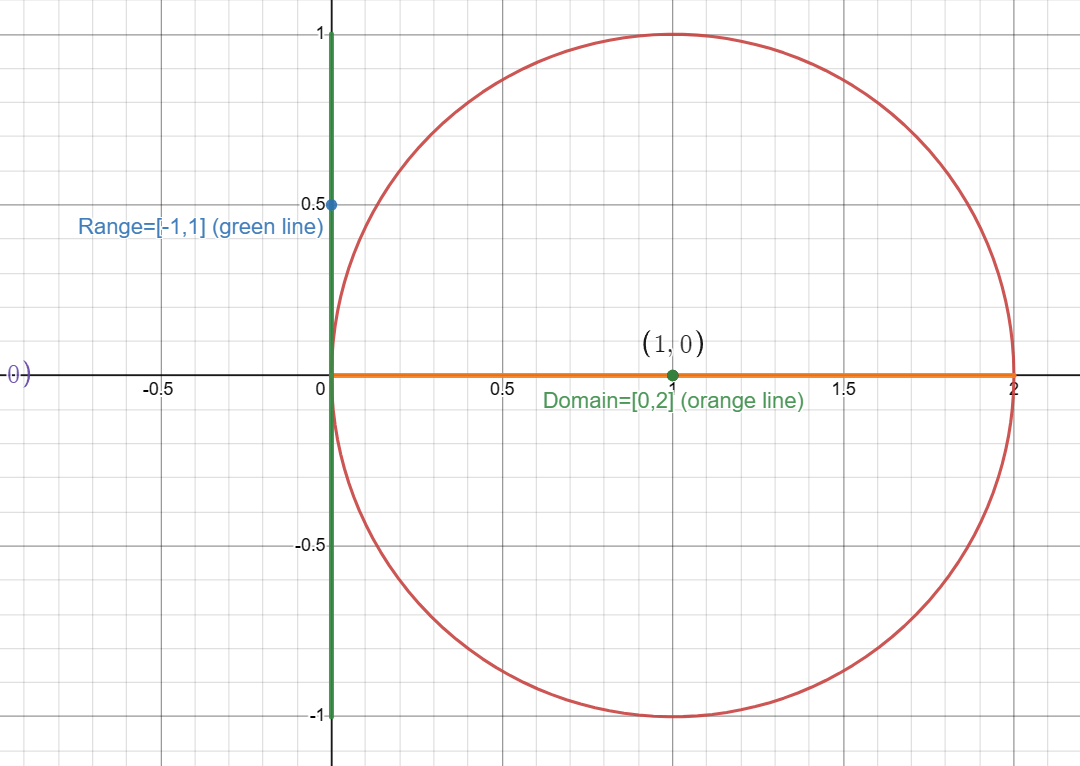
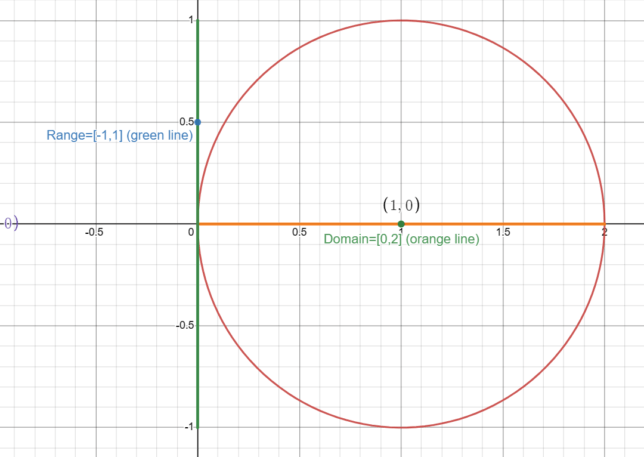
The equation (x – 1)² + y² = 1 represents a circle with a radius of 1, centered at the point (1, 0) in the Cartesian coordinate system.
Domain
The domain of the equation is the set of all possible x-values that make the equation true. For this circle, x can range from 0 to 2, inclusive. Mathematically, the domain is: 0 ≤ x ≤ 2.
Range
The range of the equation is the set of all possible y-values that make the equation true. For this circle, y can also range from -1 to 1, inclusive. Mathematically, the range is: -1 ≤ y ≤ 1.
Conclusion
The domain and range of (x – 1)² + y² = 1 are 0 ≤ x ≤ 2 and -1 ≤ y ≤ 1, respectively. These values are derived from the geometric properties of the circle, specifically its radius and center.