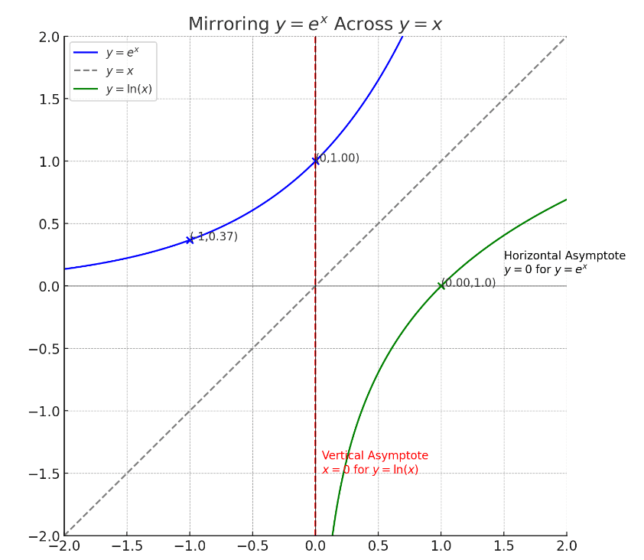
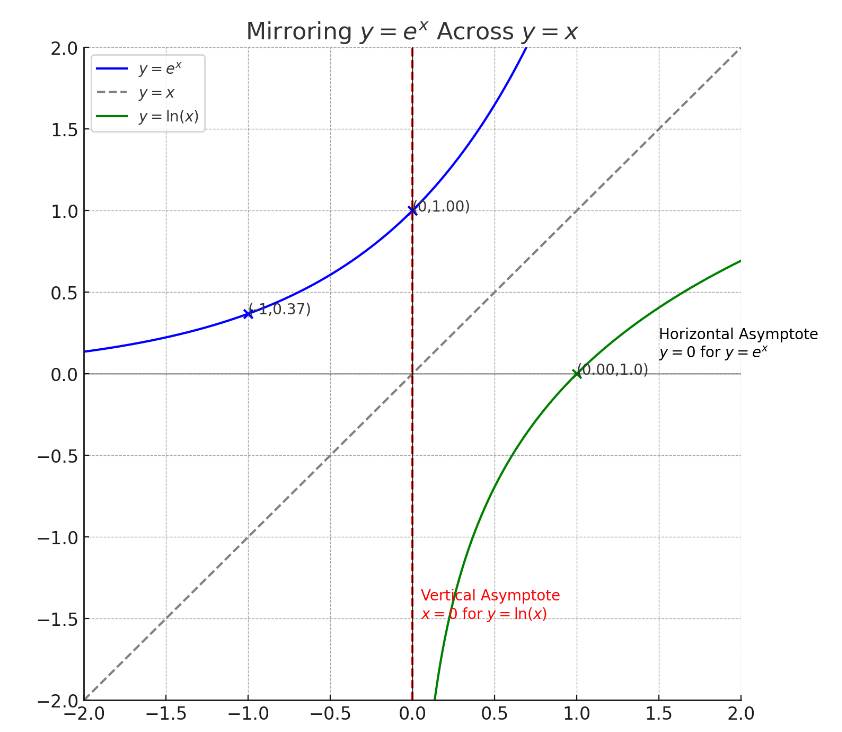
When we consider large negative values for x in the function y = eˣ:
- For x = -10, y = e⁻¹⁰ is approximately 0.0000454. This shows y is very close to 0 but not exactly 0.
- For x = -20, y = e⁻²⁰ is closer to 0, approximately 0.00000000206.
- For x = -30, y = e⁻³⁰ is about 0.0000000000009095.
As x becomes more negative, y = eˣ approaches 0 but never reaches it, demonstrating the horizontal asymptote at y = 0. This gap between the curve and the x-axis never closes, no matter how large the negative value of x.
Mirroring these points across y = x:
- The point (-10, 0.0000454) on y = eˣ mirrors to become (0.0000454, -10) on y = ln(x).
- The point (-20, 0.00000000206) mirrors to become (0.00000000206, -20).
- The point (-30, 0.0000000000009095) mirrors to become (0.0000000000009095, -30).
This illustrates how the horizontal asymptote in y = eˣ (as x approaches negative infinity) becomes a vertical asymptote in the mirrored function y = ln(x) as x approaches 0 from the right.