The document appears to be a tutorial on using linear programming to maximize profits, including detailed examples and graphs. It starts by defining a linear programming problem in two variables (x and y), where the goal is to maximize or minimize an objective function subject to a set of constraints expressed as inequalities.
The process involves several steps:
1. Writing an expression for the quantity to be maximized or minimized (objective function).
2. Determining all constraints and graphing the set of feasible points.
3. Listing the corner points of the set of feasible points.
4. Determining the value of the objective function at each corner point.
5. Selecting the maximum or minimum value of the objective function.
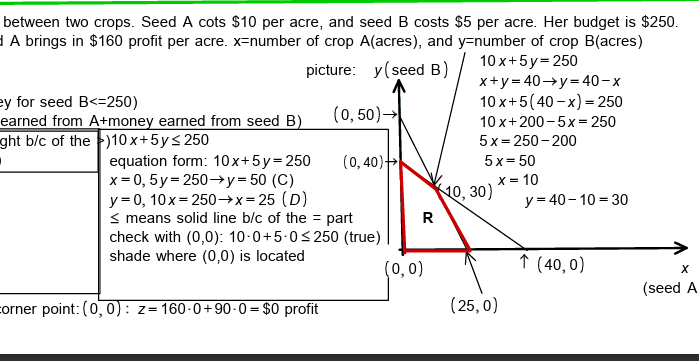
There are example problems provided, such as maximizing the objective function \( z = x + 5y \) subject to certain constraints, and real-world applications like a farmer dividing land between two crops to maximize profit given constraints on land and budget.
For example, one of the homework problems describes a farmer with 30 acres of land deciding how much to plant of crops A and B, considering the cost of seeds and the profit per acre. The problem involves setting up the constraints for land and budget, graphing the feasible region, and then finding the corner points to determine where the profit is maximized. The document provides step-by-step instructions on how to set up the equations, graph the constraints, and calculate the profits at each corner point to make the best business decision.
The document seems to serve as an educational resource for understanding and applying the principles of linear programming to real-life scenarios. It emphasizes the graphical method of solving linear programming problems, which is particularly useful for problems involving two variables, where graphical solutions are feasible and illustrative.
