Prelim example: f(x) = x² and find the slope at x=a.
Using limit formula, lim(h → 0) (f(a + h) – f(a)) / h
= lim(h → 0) ((a + h)² – a²) / h
= lim(h → 0) (a² + 2ah + h² – a²) / h
= lim(h → 0) (2ah + h²) / h
= lim(h → 0) h(2a + h) / h
= lim(h → 0) (2a + h)
= 2a + 0 = 2a
2a represents the slope on the graph of f at x=a.
Once we know the slope, we can find the equation of the tangent line. The line that touches the graph at x=a.
Let’s say we want the equation of the line at x = a = 1.
Slope at x=1 is 2(1) = 2. Equation of line y – y1 = m(x – x1)
Our m is 2. When x=1, f(1) = 1² = 1
y – 1 = 2(x – 1)
y – 1 = 2x – 2
y = 2x – 1
The equation of the tangent line is y = 2x – 1.
\[
\begin{align*}
\text{Example 2 in book:} \\
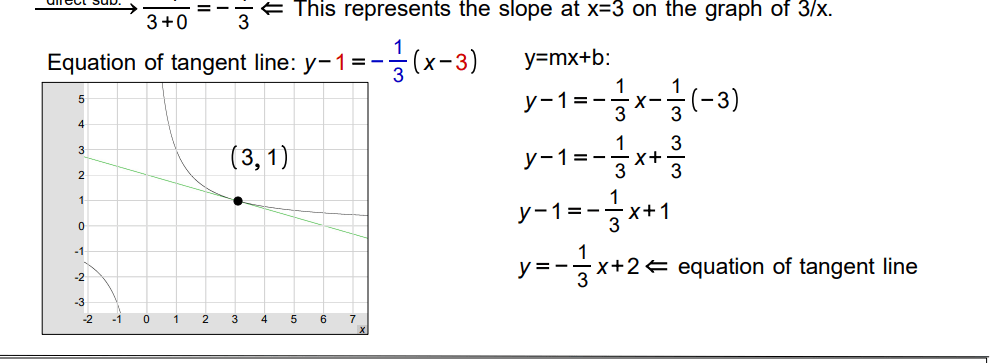
\text{Let } f(x) &= \frac{3}{x} \text{ and find slope at } (3,1) \text{ and equation of tangent line at that point.} \\
\text{Slope at } x=3 &= \lim_{{h \to 0}} \frac{\frac{3}{{3 + h}} – \frac{3}{3}}{h} \\
&= \lim_{{h \to 0}} \frac{\frac{3}{{3 + h}} – 1}{h} \\
&= \lim_{{h \to 0}} \frac{\frac{3}{{3 + h}} – \frac{{3 + h}}{{3 + h}}}{h} \\
&= \lim_{{h \to 0}} \frac{\frac{{3 – (3 + h)}}{{3 + h}}}{h} \\
&= \lim_{{h \to 0}} \frac{\frac{{-h}}{{3 + h}}}{h} \\
&= \lim_{{h \to 0}} \left( \frac{{-h}}{{3 + h}} \cdot \frac{1}{h} \right) \\
&= \lim_{{h \to 0}} \frac{{-1}}{{3 + h}} \\
&= -\frac{1}{3} \\
\text{This represents the slope at } x=3 \text{ on the graph of } \frac{3}{x}. \\
\text{Equation of tangent line: } y – 1 &= -\frac{1}{3} (x – 3) \\
y &= -\frac{1}{3} x + 2
\end{align*}
\]