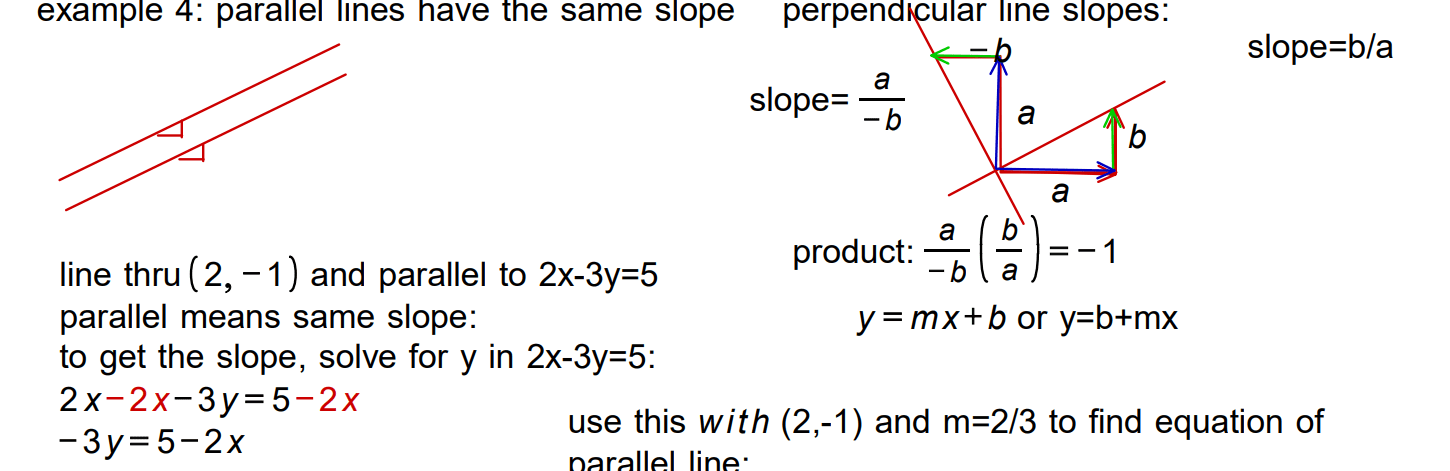Math 111 Notes for 9/25
Section 2.1: Linear Equations in Two Variables
Basic Formulas and Definitions
Standard form of a linear equation: y = mx + b
- m = slope
- b = y-intercept
Understanding Slope
Slope formula: m = (y2 – y1) / (x2 – x1)
Examples
Example 1: Graph y = 2x + 1
- Mark y-intercept (1)
- From y-intercept go 1 right
- Turn 90 degrees
- Go 2 up
- Mark the second point
- Connect points with a line
Real-World Applications
Example: Wheelchair Ramp
Recommended slope: 1/12
Actual slope: 22/288 ≈ 0.076 (less than recommended, so it’s okay)
General Form of Line
Ax + By + C = 0
Homework Solutions
[Insert your homework solutions here]Why Do Fractions Need the Same Denominator for Addition?
When adding fractions, it’s crucial that the denominators—the numbers at the bottom of the fractions—are the same. This concept is similar to stacking pieces of pie to make a column. Imagine you have slices of pie, and you want to stack them on top of each other to form a neat column. If the slices are of different sizes, they won’t stack neatly; one slice might be too large and overhang, while another might be too small and leave a gap.
In the same way, when you’re adding fractions, the denominators represent the “size” of each piece. If the denominators are different, it’s like trying to stack slices of pie of different sizes. They won’t fit together neatly to form a whole.
For example, if you have \( \frac{1}{4} \) and \( \frac{1}{5} \), you can think of these as slices of pie where one is divided into 4 equal pieces and the other is divided into 5 equal pieces. If you try to stack them together without making the sizes the same, they won’t fit neatly.
To make them fit, you need to find a common denominator, which is like resizing the slices so they are all the same size. In this case, the common denominator would be 20. You would then rewrite the fractions as \( \frac{5}{20} \) and \( \frac{4}{20} \). Now, these “slices” are the same size and can be neatly stacked (added), resulting in \( \frac{9}{20} \).
So, having the same denominator ensures that you’re adding “like to like,” making the arithmetic meaningful and accurate.