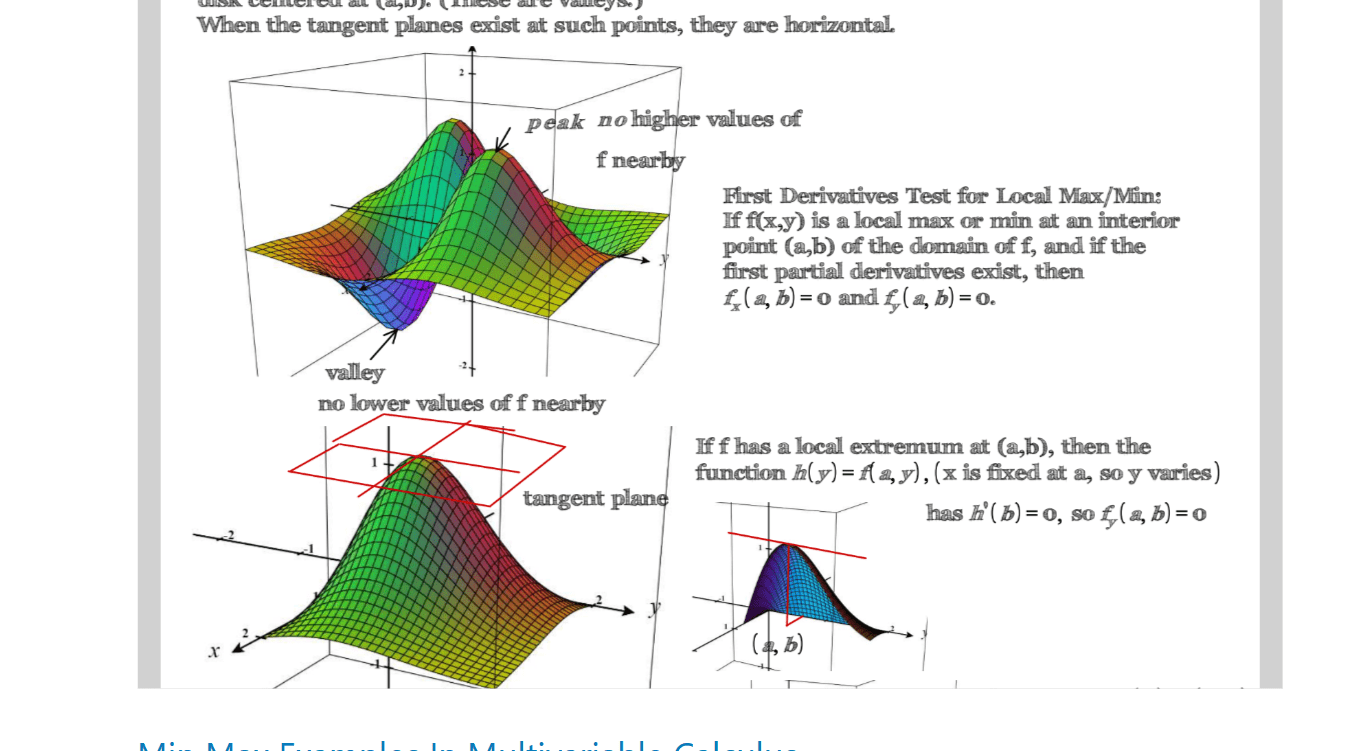
Min-Max Examples in Multivariable Calculus with Graphs
Page 1:
Discusses the function f(x, y) = x² + y² – 4x – 6y + 2 and its critical point at (2,3).
Completes the square to rewrite the function.
Concludes that the values of f get bigger and bigger, starting from z = -11 at the point (2, 3, -11).
Page 2:
Introduces the Second Partial Derivatives Test for classifying critical points.
Explains the conditions for local minima, local maxima, and saddle points.
Works through an example with f(x, y) = x⁴ + y⁴ – 4xy + 1.
Finds local minima at (1,1) and (-1,-1), and a saddle point at (0,0).
Page 3:
Discusses another example f(x, y) = 10x²y – 5x² – 4y² – x⁴ – 2y⁴.
Finds a local maximum at (0,0) and saddle points at other coordinates.
Page 4:
Discusses finding the shortest distance from a point to a plane using calculus.
Uses the function d(x, y) to represent the distance and minimizes it.