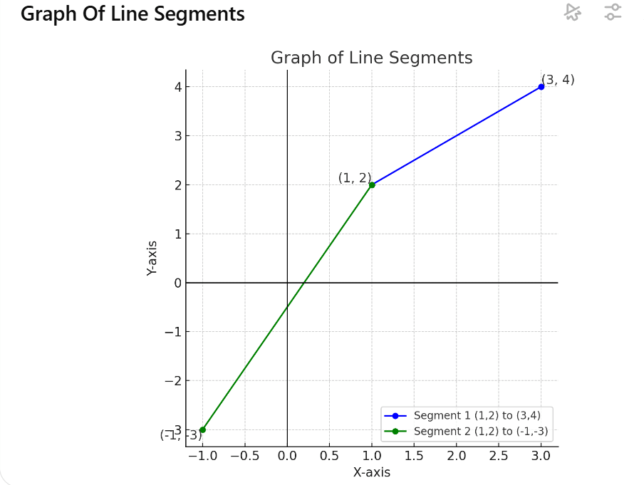
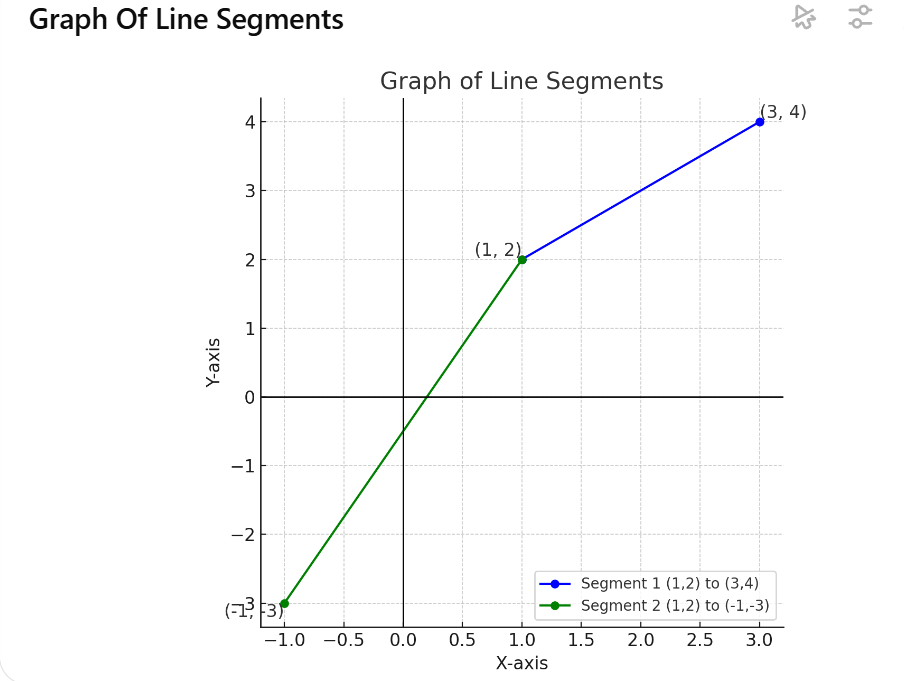
Use the distance formula between two points:
Distance = √((x₂ – x₁)² + (y₂ – y₁)²)
For points (1, 2) and (3, 4):
Length₁ = √((3 – 1)² + (4 – 2)²)
Simplify the differences:
Length₁ = √(2² + 2²)
Calculate the squares:
Length₁ = √(4 + 4)
Add the results:
Length₁ = √8
Approximate the square root:
Length₁ ≈ 2.828
Use the distance formula again for points (1, 2) and (-1, -3):
Length₂ = √((-1 – 1)² + (-3 – 2)²)
Simplify the differences:
Length₂ = √((-2)² + (-5)²)
Calculate the squares:
Length₂ = √(4 + 25)
Add the results:
Length₂ = √29
Approximate the square root:
Length₂ ≈ 5.385
Use the formula for the ratio of the two lengths:
Ratio = Length₂ ÷ Length₁
Substitute the approximate values:
Ratio = 5.385 ÷ 2.828
Perform the division:
Ratio ≈ 1.904
Thus, the approximate ratio of the lengths is 1.904.