Convergence of Sequences with Motivation, Formalism and Examples

Convergence of a Sequence

What is Convergence?

When we talk about a sequence converging, we mean that the terms in the sequence are getting closer and closer to a specific value as we go further along the sequence. This specific value is called the “limit.”

Examples

1. The Sequence 1/n:
   • Look at the terms: 1/1, 1/2, 1/3, 1/4, …
   • As the value of n (the number in the denominator) gets larger, the fraction gets smaller.
   • The terms are getting closer to 0.
   • So, this sequence converges to 0.
2. The Geometric Sequence 1/2ⁿ:
   • Look at the terms: 1/2⁰ (which is 1), 1/2¹ (which is 1/2), 1/2² (which is 1/4), …
   • Each term is half the previous term.
   • The terms are getting closer to 0.
   • So, this sequence also converges to 0.
3. The Alternating Sequence (-1)ⁿ:
   • Look at the terms: -1, 1, -1, 1, …
   • The terms keep jumping back and forth between -1 and 1.
   • There’s no single value that the terms are getting closer to.
   • So, this sequence does not converge.

Why is Convergence Important?

Understanding whether a sequence converges helps us in various fields like mathematics, physics, and engineering. It tells us how things behave as they get close to a particular point, which can be vital in many applications.

Conclusion

Convergence is about seeing how a sequence behaves as you go further along. By looking at simple examples, we can understand this concept and see how it connects to many areas of study.

Formal Definition

A sequence (a_n) is said to converge to a limit L if, for every positive number ε > 0, there exists a positive integer N such that for all n > N, the inequality |a_n – L| < ε holds.

Explanation

Let’s break down this definition into its key components and explain them:

1. Sequence (a_n): This represents the sequence we’re examining. It’s a list of numbers that follows a specific pattern, like 1, ½, ⅓, ¼, …
2. Limit L: The limit is the value that the terms of the sequence are getting closer to as n (the position in the sequence) gets larger. For example, in the sequence 1, ½, ⅓, ¼, …, the limit is 0.
3. Positive Number ε: Think of ε as a “tolerance level.” It’s a small positive number that tells us how close we want the terms of the sequence to be to the limit L.
4. Positive Integer N: This is a specific point in the sequence. After this point (for all n > N), the terms of the sequence are within our tolerance level ε of the limit L.
5. Inequality |a_n – L| < ε: This mathematical expression captures the idea of “closeness.” The absolute value |a_n – L| represents the distance between the term a_n and the limit L. We want this distance to be less than our tolerance level ε.

Intuitive Understanding

Imagine you’re on a journey towards a destination (the limit L). As you travel, you get closer and closer to your destination. The formal definition of convergence is like saying: “No matter how close you want to get to the destination (no matter how small ε is), there’s a point in your journey (a point N in the sequence) after which you’ll always be that close (or closer) to your destination.”

This concept of convergence is fundamental in calculus and analysis, and it’s used to understand how functions and sequences behave as they approach specific points or infinity.

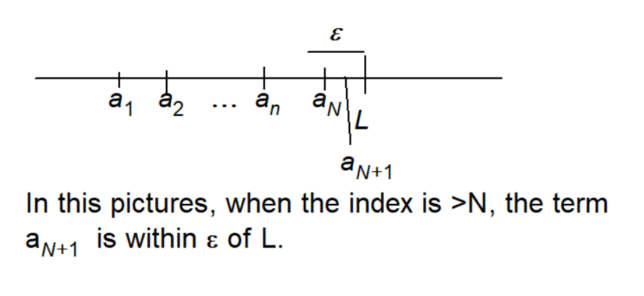
Illustration of Convergence

Let’s take the sequence (a_n) = 1/n as an example, and we’ll illustrate how it converges to the limit L = 0.

Step 1: Choose a Tolerance Level ε

Suppose we choose ε = 0.1. This is our tolerance level, meaning we want to find an index in the sequence where all the terms are within 0.1 of the limit 0. The choice of ε is arbitrary; it represents how close we want to get to the limit.

Step 2: Find the Index N

We need to find a positive integer N such that for all n > N, the inequality |a_n – L| < ε holds. In this case, we want to find N such that for all n > N, |1/n – 0| < 0.1.

For our sequence, we can choose N = 10. This means that starting from the 11th term in the sequence (index n = 11), the value 1/n is less than 0.1.

Step 3: Verify the Inequality

Now, we can verify that for all n > 10, the inequality |1/n – 0| < 0.1 holds. For example:

• For n = 11, |1/11 – 0| = 0.0909… < 0.1
• For n = 12, |1/12 – 0| = 0.0833… < 0.1
• And so on…

Conclusion

The sequence (a_n) = 1/n converges to the limit L = 0. We’ve shown that no matter how close we want to get to the limit (no matter how small ε is), there’s an index in the sequence (N) after which all the terms are within our chosen tolerance level of the limit.

The choice of ε was arbitrary, and the value of N depended on our choice of ε. The specific values used here were for illustration purposes, and the process would be similar for other choices of ε and corresponding values of N.

Illustration of Convergence

Consider the sequence (a_n) = 1/n². We’ll illustrate how it converges to the limit L = 0.

Step 1: Choose a Tolerance Level ε

Suppose we choose ε = 0.01. This is our tolerance level, meaning we want to find an index in the sequence where all the terms are within 0.01 of the limit 0.

Step 2: Find the Index N

We need to find a positive integer N such that for all n > N, the inequality |a_n – L| < ε holds. In this case, we want to find N such that for all n > N, |1/n² – 0| < 0.01.

To find N, we need to solve the inequality 1/n² < 0.01:

• 1/n² < 0.01
• n² > 100
• n > 10

So we can choose N = 10.

Step 3: Verify the Inequality

Now, we can verify that for all n > 10, the inequality |1/n² – 0| < 0.01 holds. For example:

• For n = 11, |1/11² – 0| = 0.0083… < 0.01
• For n = 12, |1/12² – 0| = 0.0069… < 0.01
• And so on…

Conclusion

The sequence (a_n) = 1/n² converges to the limit L = 0. By choosing a specific tolerance level ε and solving the corresponding inequality, we found the index N after which all terms in the sequence are within our chosen tolerance level of the limit.

Convergence of the Sequence (-1)ⁿ

The sequence (-1)ⁿ is an example of a sequence that does not converge. Let’s analyze this using the formal definition of convergence:

A sequence (aₙ) converges to a limit L if for every ε > 0, there exists a positive integer N such that for all n > N, |aₙ – L| < ε.

In the case of the sequence (-1)ⁿ, the terms alternate between -1 and 1. This means that no matter what value of L we choose, we cannot find a positive integer N that satisfies the condition |aₙ – L| < ε for all n > N and for all ε > 0.

For example, if we choose ε = 0.5 and try to find a value of N that works:

• If n is even, then (-1)ⁿ = 1, so if we choose L = 1, then |aₙ – L| = 0 < ε.
• However, if n is odd, then (-1)ⁿ = -1, so |aₙ – L| = 2 > ε.

Since we cannot find a value of N that works for all n > N and for all ε > 0, the sequence (-1)ⁿ does not converge.

This example illustrates the importance of the formal definition of convergence. Even though the terms of the sequence are bounded (they do not grow without bound), the sequence does not converge because it does not approach a specific limit.

Rules of Limits for Sequences

When working with sequences, we often need to find the limit of a sequence as it approaches infinity. The following rules can help us find these limits:

• Sum Rule: \(\lim (a_n + b_n) = \lim a_n + \lim b_n\)
• Difference Rule: \(\lim (a_n – b_n) = \lim a_n – \lim b_n\)
• Product Rule: \(\lim (a_n \cdot b_n) = \lim a_n \cdot \lim b_n\)
• Quotient Rule: \(\lim \left(\frac{a_n}{b_n}\right) = \frac{\lim a_n}{\lim b_n}\), provided \(\lim b_n \neq 0\)
• Constant Multiple Rule: \(\lim (c \cdot a_n) = c \cdot \lim a_n\)
• Power Rule: \(\lim (a_n^k) = (\lim a_n)^k\)
• Root Rule: \(\lim \sqrt[k]{a_n} = \sqrt[k]{\lim a_n}\)

These rules are based on the assumption that the limits of the individual sequences exist. If the limits do not exist, then these rules may not apply.

By using these rules, we can often find the limit of a complex sequence by breaking it down into simpler parts and applying the rules to each part.